
| A. | 12 | B. | 20 | C. | 16 | D. | 32 |
分析 由函数为奇函数得到a,b的关系式,结合不等式的性质求出ab的最小值,代入f(1)得答案.
解答 解:∵函数f(x)=(ab-a-4b-5)x2+$\frac{a+4b}{x}$(a>0,b>0)为奇函数,
∴f(-x)+f(x)=0,即(ab-a-4b-5)x2-$\frac{a+4b}{x}$+(ab-a-4b-5)x2+$\frac{a+4b}{x}$=0.
∴2(ab-a-4b-5)x2 =0,则ab-a-4b-5=0.
即ab-5=a+4b,
∵a>0,b>0,
∴ab-5$≥2\sqrt{4ab}=4\sqrt{ab}$,
∴ab-4$\sqrt{ab}$-5≥0,
解得:$\sqrt{ab}≤-1$(舍)或$\sqrt{ab}≥5$.
则ab≥25.
∴f(1)=ab-a-4b-5+a+4b=ab-5≥25-5=20.
故选:B.
点评 本题考查函数的奇偶性的性质,训练了不等式性质的应用及一元二次不等式的解法,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{7}$ | B. | -$\frac{3}{7}$ | C. | -$\frac{7}{3}$ | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北冀州市高二文上月考三数学试卷(解析版) 题型:选择题
已知函数 ,若
,若 ,
, ,
, 互不相等,且
互不相等,且 ,则
,则 的取值范围是( )
的取值范围是( )
A.(10,12) B.(5,6)
C.(1,10) D.(20,24)
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广西陆川县中学高二理9月月考数学试卷(解析版) 题型:解答题
已知圆 :
: .
.
(1)直线 过点
过点 ,且与圆
,且与圆 交于
交于 两点,若
两点,若 ,求直线
,求直线 的方程;
的方程;
(2)过圆 上一动点
上一动点 作平行于
作平行于 轴的直线
轴的直线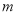 ,设
,设 与
与 轴的交点为
轴的交点为 ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com