练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究，在饲料充足的前提下，兴趣小组对饲养时间x（单位：月）与这种鱼类的平均体重y（单位：千克）得到一组观测值，如下表：

    xi（月）

    1

    2

    3

    4

    5

    yi（千克）

    0.5

    0.9

    1.7

    2.1

    2.8

    （参考公式： = ， = ﹣ ）

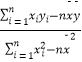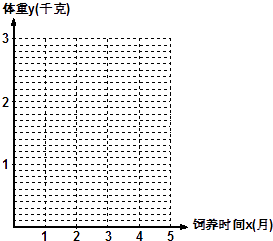
    （1）在给出的坐标系中，画出关于x，y两个相关变量的散点图．
    （2）请根据上表提供的数据，用最小二乘法求出变量y关于变量x的线性回归直线方程 ．
    （3）预测饲养满12个月时，这种鱼的平均体重（单位：千克）

    【答案】
    （1）解：散点图如图所示


    （2）解：由题设 =3， =1.6，

    ∴ = = =0.58，

    a= ﹣ =﹣0.14

    故回归直线方程为y=0.58x﹣0.14


    （3）解：当x=12时，y=0.58×12﹣0.14=6.82

    饲养满12个月时，这种鱼的平均体重约为6.82千克


    【解析】（1）利用所给数据，可得散点图；（2）利用公式，计算回归系数，即可得到回归方程；（3）x=12代入回归方程，即可得到结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，网格纸上小正方形的边长为，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设有两个命题：p：关于x的不等式x2＋2x－4－a≥0对一切x∈R恒成立；q：已知a≠0，a≠±1，函数y＝－|a|x在R上是减函数，若p∧q为假命题，p∨q为真命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（cos x，sin x）， =（cos x，﹣sin x），且x∈[0， ]．求：
    （1）及 ；
    （2）若f（x）= ﹣2λ 的最小值是﹣ ，求λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）求函数的单调区间；

    （2）若，证明：对任意的实数，都有.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设{an}是由正数组成的等比数列，公比q=2，且a1a2a3…a30=230 ， 那么a3a6a9…a30等于（ ）
    A.210
    B.220
    C.216
    D.215

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的前n项和为Sn=2n2 ， {bn}为等比数列，且a1=b1 ， b2（a2﹣a1）=b1 ．
    （1）求数列{an}和{bn}的通项公式；
    （2）设cn= ，求数列{cn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝ax2＋1(a>0)，g(x)＝x3＋bx.

    (1)若曲线y＝f(x)与曲线y＝g(x)在它们的交点(1，c)处具有公共切线，求a，b的值；

    (2)当a＝3，b＝－9时，若函数f(x)＋g(x)在区间[k，2]上的最大值为28，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （Ⅰ）当时，求在处的切线方程；

    （Ⅱ）若且函数有且仅有一个零点，求实数的值；

    （Ⅲ）在（Ⅱ）的条件下，若时， 恒成立，求实数的取值范围．

    查看答案和解析>>

    同步练习册答案