
 +
+ 与
与 -
- 垂直;
垂直; ,∠COB=θ,θ∈(-
,∠COB=θ,θ∈(- ,
, ),
), •
• =
= ,求cosθ.
,求cosθ. +
+ 与
与 -
- 垂直,只需证明(
垂直,只需证明( +
+ )•(
)•( -
- )=0即可;
)=0即可; •
• =
= 可求出cos(θ-
可求出cos(θ- ),然后根据cosθ=cos[(θ-
),然后根据cosθ=cos[(θ- )+
)+ ],利用余弦的两角和公式进行求解.
],利用余弦的两角和公式进行求解. |=|
|=| |=1,
|=1, +
+ )•(
)•( -
- )=
)= 2-
2- 2
2 |2-|
|2-| |2=1-1=0,
|2=1-1=0, +
+ 与
与 -
- 垂直.
垂直. =(cos
=(cos ,sin
,sin ),
), =(cosθ,sinθ),
=(cosθ,sinθ), •
• =cos
=cos cosθ+sin
cosθ+sin sinθ=cos(θ-
sinθ=cos(θ- ),
), •
• =
= ,∴cos(θ-
,∴cos(θ- )=
)= ,
, <θ<
<θ< ,
, <θ-
<θ- <0,
<0, )=-
)=- =-
=- ,
, )+
)+ ]
] )cos
)cos -sin(θ-
-sin(θ- )sin
)sin
 ×
× -(-
-(- )×
)× =
= .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 4 | ab |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| PA |
| PB |
| AB |
| AP |
| PB |
| AB |
| PA |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| PA |
| PB |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年重庆市永川区景圣中学高三(下)第三次月考数学试卷(解析版) 题型:选择题
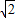
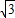
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com