
【题目】已知函数f(x)=cos2x+2![]() sinxcosx﹣sin2x.
sinxcosx﹣sin2x.
(1)求函数f(x)的最小正周期
(2)求函数f(x)单调增区间.
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
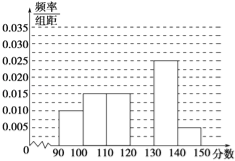
(1)求分数在[120,130)内的频率;
(2)若在同一组数据中,将该组区间的中点值(如:组区间[100,110)的中点值为![]() =105)作为这组数据的平均分,据此,估计本次考试的平均分;
=105)作为这组数据的平均分,据此,估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 称为
称为![]() ,
,![]() 的二维平方平均数,
的二维平方平均数,![]() 称为
称为![]() ,
,![]() 的二维算术平均数,
的二维算术平均数,![]() 称为
称为![]() ,
,![]() 的二维几何平均数,
的二维几何平均数,![]() 称为
称为![]() ,
,![]() 的二维调和平均数,其中
的二维调和平均数,其中![]() ,
,![]() 均为正数.
均为正数.
(1)试判断![]() 与
与![]() 的大小,并证明你的猜想.
的大小,并证明你的猜想.
(2)令![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 的大小,并证明你的猜想.
的大小,并证明你的猜想.
(3)令![]() ,
,![]() ,
,![]() ,试判断
,试判断![]() 、
、![]() 、
、![]() 三者之间的大小关系,并证明你的猜想.
三者之间的大小关系,并证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具所需成本费用为P元,且P=1 000+5x+![]() x2,而每套售出的价格为Q元,其中Q(x)=a+
x2,而每套售出的价格为Q元,其中Q(x)=a+![]() (a,b∈R),
(a,b∈R),
(1)问:玩具厂生产多少套时,使得每套所需成本费用最少?
(2)若生产出的玩具能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求a,b的值.(利润=销售收入-成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:![]() ,直线l:
,直线l:![]() ,下列四个选项,其中正确的是( )
,下列四个选项,其中正确的是( )
A.对任意实数k与θ,直线l和圆M有公共点
B.存在实数k与θ,直线l和圆M相离
C.对任意实数k,必存在实数θ,使得直线l与圆M相切
D.对任意实数θ,必存在实数k,使得直线l与圆M相切
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆E经过M(﹣1,0),N(0,1),P(![]() ,
,![]() )三点.
)三点.
(1)求圆E的方程;
(2)若过点C(2,2)作圆E的两条切线,切点分别是A,B,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆的中心在原点,焦点在![]() 轴上,长轴长是短轴长的2倍且经过点
轴上,长轴长是短轴长的2倍且经过点![]() ,平行于
,平行于![]() 的直线
的直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,直线
,直线![]() 交椭圆于
交椭圆于![]() 两个不同点.
两个不同点.
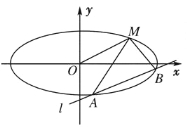
(1)求椭圆的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点C在直线3x﹣y=0上,顶点A、B的坐标分别为(4,2),(0,5).
(Ⅰ)求过点A且在x,y轴上的截距相等的直线方程;
(Ⅱ)若△ABC的面积为10,求顶点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如下表.
非一线城市 | 一线城市 | 总计 | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
总计 | 58 | 42 | 100 |
附表:
|
|
|
|
|
|
|
|
|
|
由![]() 算得,
算得,![]() ,
,
参照附表,得到的正确结论是
A. 在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关”
C. 有99%以上的把握认为“生育意愿与城市级别有关”
D. 有99%以上的把握认为“生育意愿与城市级别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com