
【题目】已知函数![]() .
.
(1)若![]() 存在极值,求实数a的取值范围;
存在极值,求实数a的取值范围;
(2)设![]() ,设
,设![]() 是定义在
是定义在![]() 上的函数.
上的函数.
(ⅰ)证明:![]() 在
在![]() 上为单调递增函数(
上为单调递增函数(![]() 是
是![]() 的导函数);
的导函数);
(ⅱ)讨论![]() 的零点个数.
的零点个数.
【答案】(1)![]() .(2)(ⅰ)证明见解析;(ⅱ)答案见解析
.(2)(ⅰ)证明见解析;(ⅱ)答案见解析
【解析】
(1)求导得![]() ,按照
,按照![]() 、
、![]() 分类,求得
分类,求得![]() 、
、![]() 的解集即可得解;
的解集即可得解;
(2)(ⅰ)令![]() ,对
,对![]() 求导,按照
求导,按照![]() 、
、![]() 分类,证明
分类,证明![]() 恒大于0,即可得证;
恒大于0,即可得证;
(ⅱ)由![]() 的单调性结合
的单调性结合![]() ,按照
,按照![]() 、
、![]() 分类,结合
分类,结合![]() 即可得解.
即可得解.
(1)求导得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在R上单调递减,
在R上单调递减,![]() 无极值;
无极值;
当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增,
上单调递增,
则![]() 在
在![]() 处有极小值.
处有极小值.
综上,实数a的取值范围为![]() ;
;
(2)(ⅰ)证明:由题意![]() ,
,
∵令![]() ,
,
∴![]() ,
,
∵![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
则![]() ;
;
当![]() 时,令
时,令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() ,
,
从而有:![]() ,而
,而![]() ,
,
则![]() ,则
,则![]() ;
;
综上,对![]() 都有
都有![]() 成立,
成立,
故![]() 在区间
在区间![]() 单调递增;
单调递增;
(ⅱ)由(ⅰ)知,![]() 在区间
在区间![]() 单调递增且
单调递增且![]() ,
,
①当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 则
则![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 则
则![]() 在
在![]() 单调递增,
单调递增,
则![]() 是
是![]() 的唯一极小值点,且
的唯一极小值点,且![]() ,
,
从而可知:当![]() 时,
时,![]() 在区间
在区间![]() 有唯一零点0;
有唯一零点0;
②当![]() 时,有
时,有![]() ,
,
且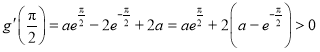 ,
,
故存在![]() 使
使![]() ,
,
此时![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
且![]()
![]() ,
,
又![]() ,由零点存在定理知:
,由零点存在定理知:
则![]() 在区间
在区间![]() 有唯一零点,记作
有唯一零点,记作![]() ,
,
从而可知:当![]() 时,
时,![]() 在区间
在区间![]() 上有两个零点:0和
上有两个零点:0和![]() ;
;
综上:①当![]() 时,
时,![]() 在区间
在区间![]() 有唯一零点0;
有唯一零点0;
②当![]() 时,
时,![]() 在区间
在区间![]() 有两个不同零点.
有两个不同零点.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】设X是有限集,t为正整数,F是包含t个子集的子集族:F=![]() .如果F中的部分子集构成的集族S满足:对S中任意两个不相等的集合A、B,
.如果F中的部分子集构成的集族S满足:对S中任意两个不相等的集合A、B,![]() 均不成立,则称S为反链.设S1为包含集合最多的反链,S2是任意反链.证明:存在S2到S1的单射f,满足
均不成立,则称S为反链.设S1为包含集合最多的反链,S2是任意反链.证明:存在S2到S1的单射f,满足![]() 或
或![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】庄子说:“一尺之锤,日取其半,万世不竭”,这句话描述的是一个数列问题,现用程序框图描述,如图所示,若输入某个正整数n后,输出的S∈(![]() ,
,![]() ),则输入的n的值为( )
),则输入的n的值为( )
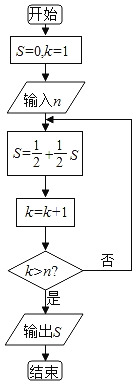
A.7B.6C.5D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=axlnx﹣x2﹣ax+1(a∈R)在定义域内有两个不同的极值点.
(1)求实数a的取值范围;
(2)设两个极值点分别为x1,x2,x1<x2,证明:f(x1)+f(x2)<2﹣x12+x22.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上的动点,
是椭圆上的动点,![]() 的最大面积是
的最大面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆E经过椭圆的左、右焦点,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,
三点共线,![]() 为坐标原点,直线
为坐标原点,直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,且
,且![]() .
.
(i) 求直线![]() 的斜率;
的斜率;
(ii)当![]() 的面积取到最大值时,求直线
的面积取到最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() 过原点的直线与椭圆交于A,B两点(点A在第一象限),过点A作x轴的垂线,垂足为点
过原点的直线与椭圆交于A,B两点(点A在第一象限),过点A作x轴的垂线,垂足为点![]() ,设直线BE与椭圆的另一交点为P,连接AP得到直线l,交x轴于点M,交y轴于点N.
,设直线BE与椭圆的另一交点为P,连接AP得到直线l,交x轴于点M,交y轴于点N.
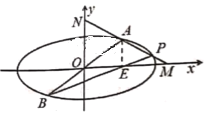
(1)若![]() ,求直线AP的斜率;
,求直线AP的斜率;
(2)记![]() 的面积分别为S1,S2,S3,求
的面积分别为S1,S2,S3,求![]() 的的最大值.
的的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() (a>b>0)的左、右焦点分别为F1,F2,过点F2的直线交椭圆于M,N两点.已知椭圆的短轴长为
(a>b>0)的左、右焦点分别为F1,F2,过点F2的直线交椭圆于M,N两点.已知椭圆的短轴长为![]() ,离心率为
,离心率为![]() .
.

(1)求椭圆的标准方程;
(2)当直线MN的斜率为![]() 时,求
时,求![]() 的值;
的值;
(3)若以MN为直径的圆与x轴相交的右交点为P(t,0),求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年新冠肺炎疫情期间,某区政府为了解本区居民对区政府防疫工作的满意度,从本区居民中随机抽取若干居民进行评分(满分
年新冠肺炎疫情期间,某区政府为了解本区居民对区政府防疫工作的满意度,从本区居民中随机抽取若干居民进行评分(满分![]() 分).根据调查数据制成如下表格和频率分布直方图.已知评分在
分).根据调查数据制成如下表格和频率分布直方图.已知评分在![]() 的居民有
的居民有![]() 人.
人.
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
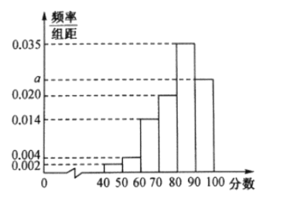
(1)求频率分布直方图中![]() 的值及所调查的总人数;
的值及所调查的总人数;
(2)定义满意度指数![]() (满意程度的平均分)/100,若
(满意程度的平均分)/100,若![]() ,则防疫工作需要进行大的调整,否则不需要大调整.根据所学知识判断该区防疫工作是否需要进行大调整?
,则防疫工作需要进行大的调整,否则不需要大调整.根据所学知识判断该区防疫工作是否需要进行大调整?
(3)为了解部分居民不满意的原因,从不满意的居民(评分在![]() 、
、![]() )中用分层抽样的方法抽取
)中用分层抽样的方法抽取![]() 名居民,倾听他们的意见,并从
名居民,倾听他们的意见,并从![]() 人中抽取
人中抽取![]() 人担任防疫工作的监督员,求这
人担任防疫工作的监督员,求这![]() 人中仅有一人对防疫工作的评分在
人中仅有一人对防疫工作的评分在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com