
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
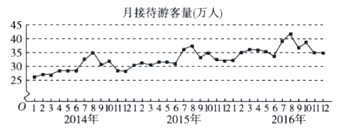
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数).
为常数).
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)是否存在正实数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,若存在,求出实数
,若存在,求出实数![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(Ⅲ)当![]() 时,
时, ![]() ,对
,对![]() 恒成立,求整数
恒成立,求整数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,每年投入固定成本0.5万元,此外每生产100件这种产品还需要增加投资0.25万元,经预测可知,市场对这种产品的年需求量为500件,当出售的这种产品的数量为t(单位:百件)时,销售所得的收入约为![]() (万元).
(万元).
(1)若该公司的年产量为x(单位:百件),试把该公司生产并销售这种产品所得的年利润表示为年产量x的函数;
(2)当这种产品的年产量为多少时,当年所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:![]() 与拋物线C:
与拋物线C:![]() 相切.
相切.
(1)求拋物线方程;
(2)斜率不为0的直线![]() 经过拋物线C的焦点F,交抛物线于两点A,B,拋物线C上是否存在两点D,E关于直线
经过拋物线C的焦点F,交抛物线于两点A,B,拋物线C上是否存在两点D,E关于直线![]() 对称.若存在求出斜率k的取值范围;若不存在,说明理由.
对称.若存在求出斜率k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的方程和圆
的方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 为圆
为圆![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的有( )
A.设正六棱锥的底面边长为1,侧棱长为![]() ,那么它的体积为
,那么它的体积为![]()
B.用斜二测法作△ABC的水平放置直观图得到边长为a的正三角形,则△ABC面积为![]()
C.三个平面可以将空间分成4,6,7或者8个部分
D.已知四点不共面,则其中任意三点不共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆O及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转
旋转![]() 而成,如图2.已知圆O的半径为
而成,如图2.已知圆O的半径为![]() ,设
,设![]() ,
,![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() (S圆锥的侧面积
(S圆锥的侧面积![]() (R-底面圆半径,I-母线长))
(R-底面圆半径,I-母线长))
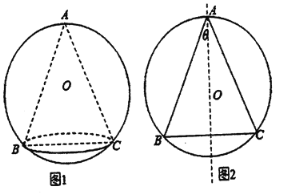
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积S最大.求S取得最大值时腰![]() 的长度
的长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com