
 ,且经过这三个点的小圆周长为4π,则R=( )
,且经过这三个点的小圆周长为4π,则R=( )


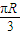 ,得出AB=BC=CA=R,利用其周长得到正三角形ABC的外接圆半径r=2,故可以得到高,设D是BC的中点,在△OBC中,又可以得到角以及边与R的关系,在Rt△ABD中,再利用直角三角形的勾股定理,即可解出R.
,得出AB=BC=CA=R,利用其周长得到正三角形ABC的外接圆半径r=2,故可以得到高,设D是BC的中点,在△OBC中,又可以得到角以及边与R的关系,在Rt△ABD中,再利用直角三角形的勾股定理,即可解出R.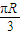 ,
,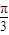 ,
, r=3,D是BC的中点.
r=3,D是BC的中点.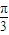 ,所以BC=BO=R,BD=
,所以BC=BO=R,BD= BC=
BC= R.
R. R2+9,所以R=2
R2+9,所以R=2 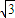 .
.

 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源:重庆三模 题型:单选题
| πR |
| 3 |
A.4
| B.2
| C.2 | D.
|
查看答案和解析>>
科目:高中数学 来源:2011年重庆市高考数学三模试卷(理科)(解析版) 题型:选择题
 ,且经过这三个点的小圆周长为4π,则R=( )
,且经过这三个点的小圆周长为4π,则R=( )


查看答案和解析>>
科目:高中数学 来源:0124 期末题 题型:单选题
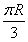 ,且经过这三个点的小圆周长为4π,则R=
,且经过这三个点的小圆周长为4π,则R=[ ]
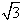
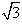
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com