(1)解:函数f(x)的定义域为(0,+∞),
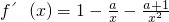
=
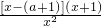
(2分)
∵x>0,a>0,
∴由f′(x)≥0得x≥a+1,f′(x)≤0得x≤a+1,
∴f(x)在(0,a+1)上递减,在(a+1,+∞)上递增.(4分)
(2)解:∵a∈N
*,∴由(1)知f
min=f(a+1)=a+2-aln(a+1)
∵f(x)有零点,
∴有a+2-aln(a+1)≤0,得ln(a+1)-(1+

)≥0
令u(a)=ln(a+1)-(1+

),易知u(a)在定义域内是增函数;(6分)
∵u(3)=ln4-

<0,∴
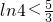
,∴4<
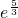
,∴4
3<e
5,而e
5>4
3成立,∴u(3)<0
u(4)=ln5-

>0,∴5
2>e
3,而5
2>e
3成立,∴u(4)>0
故使函数f(x)有零点的最小正整数a的值为4.(8分)
(3)证明:由(2)知ln(a+1)-(1+

)≥0,即ln(a+1)≥(1+

),(a≥4),
∴lnn>1+
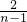
(n∈N
*,n≥5),ln(n
2)>1+
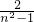
)(n∈N
*,n≥3),
即lnn>

(n∈N
*,n≥3),(11分)
∴ln3+ln4+…+lnn>

(n-2)+
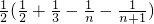
即
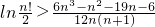
∴ln(n!)-ln2>
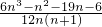
(n∈N
*,n≥3).(13分)
分析:(1)确定函数f(x)的定义域为(0,+∞),求导函数,即可确定f(x)的单调区间;
(2)先求f
min=f(a+1)=a+2-aln(a+1),再利用f(x)有零点,可得ln(a+1)-(1+

)≥0,构建函数u(a)=ln(a+1)-(1+

),易知u(a)在定义域内是增函数,从而可求函数f(x)有零点的最小正整数a的值;
(3)先证明ln(a+1)≥(1+

),进而有lnn>

(n∈N
*,n≥3),从而可得ln3+ln4+…+lnn>

(n-2)+
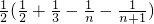
,故可得证.
点评:本题以函数为载体,考查函数的单调性,考查函数的零点,考查不等式的证明,用好导数是关键.

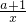 (a>0)
(a>0)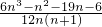 (n∈N*,n≥3).
(n∈N*,n≥3).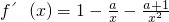 =
=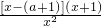 (2分)
(2分) )≥0
)≥0 ),易知u(a)在定义域内是增函数;(6分)
),易知u(a)在定义域内是增函数;(6分) <0,∴
<0,∴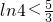 ,∴4<
,∴4<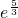 ,∴43<e5,而e5>43成立,∴u(3)<0
,∴43<e5,而e5>43成立,∴u(3)<0 >0,∴52>e3,而52>e3成立,∴u(4)>0
>0,∴52>e3,而52>e3成立,∴u(4)>0 )≥0,即ln(a+1)≥(1+
)≥0,即ln(a+1)≥(1+ ),(a≥4),
),(a≥4),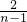 (n∈N*,n≥5),ln(n2)>1+
(n∈N*,n≥5),ln(n2)>1+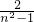 )(n∈N*,n≥3),
)(n∈N*,n≥3), (n∈N*,n≥3),(11分)
(n∈N*,n≥3),(11分) (n-2)+
(n-2)+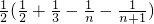
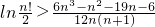
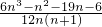 (n∈N*,n≥3).(13分)
(n∈N*,n≥3).(13分) )≥0,构建函数u(a)=ln(a+1)-(1+
)≥0,构建函数u(a)=ln(a+1)-(1+ ),易知u(a)在定义域内是增函数,从而可求函数f(x)有零点的最小正整数a的值;
),易知u(a)在定义域内是增函数,从而可求函数f(x)有零点的最小正整数a的值; ),进而有lnn>
),进而有lnn> (n∈N*,n≥3),从而可得ln3+ln4+…+lnn>
(n∈N*,n≥3),从而可得ln3+ln4+…+lnn> (n-2)+
(n-2)+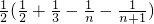 ,故可得证.
,故可得证.
