
分析 (1)由题意知抛物线方程为y2=x,联立直线l:y=x-2,结合韦达定理和中点坐标公式,可得答案.
(2)解方程组$\left\{\begin{array}{l}{y}^{\;}=2x\\{y}^{2}=2px\end{array}\right.$得P($\frac{p}{2}$,p),M(2,0),由此可知当p变化时,点Q在一条定直线y=-4上.
解答 解:(1)若抛物线焦点坐标为($\frac{1}{4}$,0),则$\frac{p}{2}$=$\frac{1}{4}$,
∴2p=1,
故抛物线C的方程为:y2=x,
由$\left\{\begin{array}{l}{y}^{\;}=x-2\\{y}^{2}=x\end{array}\right.$得:y2-y-2=0,
故y1+y2=2,即弦AB的中点纵坐标为$\frac{1}{2}$,
代入直线l方程可得:x=$\frac{5}{2}$,
故AB的中点坐标为:($\frac{5}{2}$,$\frac{1}{2}$)
证明:(2)解方程组$\left\{\begin{array}{l}{y}^{\;}=2x\\{y}^{2}=2px\end{array}\right.$得P($\frac{p}{2}$,p),M(2,0)
PQ直线方程为y=$\frac{2p}{p-4}$(x-2)与抛物线y2=2px交点Q纵坐标为-4
当p变化时,点Q在一条定直线y=-4上.
点评 本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解答.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一实根 | B. | 至多有一实根 | C. | 没有实根 | D. | 必有唯一的实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
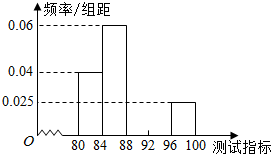 某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:
某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:| 组号 | 测试指标 | 频数 | 频率 |
| 第一组 | [80,84] | 8 | 0.16 |
| 第二组 | [84,88] | x | 0.24 |
| 第三组 | [88,92] | 15 | p |
| 第四组 | [92,96] | 10 | q |
| 第五组 | [96,100] | y | 0.1 |
| 合 计 | 50 | 1 | |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com