
ΓΨΧβΡΩΓΩ“―÷Σ¥”![]() ΒΊΒΫ
ΒΊΒΫ![]() ΒΊΙ≤”–ΝΫΧθ¬ΖΨΕ
ΒΊΙ≤”–ΝΫΧθ¬ΖΨΕ![]() ΚΆ
ΚΆ![]() Θ§ΨίΆ≥ΦΤΘ§Ψ≠ΙΐΝΫΧθ¬ΖΨΕΥυ”ΟΒΡ ±ΦδΜΞ≤Μ”ΑœλΘ§«“Ψ≠Ιΐ
Θ§ΨίΆ≥ΦΤΘ§Ψ≠ΙΐΝΫΧθ¬ΖΨΕΥυ”ΟΒΡ ±ΦδΜΞ≤Μ”ΑœλΘ§«“Ψ≠Ιΐ![]() ΚΆ
ΚΆ![]() Υυ”Ο ±Φδ¬δ‘ΎΗς ±ΦδΕΈΡΎΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΖ÷±πΈΣœ¬ΆΦΘ®1Θ©ΚΆΘ®2Θ©ΓΘ
Υυ”Ο ±Φδ¬δ‘ΎΗς ±ΦδΕΈΡΎΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΖ÷±πΈΣœ¬ΆΦΘ®1Θ©ΚΆΘ®2Θ©ΓΘ

œ÷ΦΉΓΔ““ΝΫ»ΥΖ÷±π”–40Ζ÷÷”ΚΆ50Ζ÷÷” ±Φδ”Ο”Ύ¥”![]() ΒΊΒΫ
ΒΊΒΫ![]() ΒΊΓΘ
ΒΊΓΘ
Θ®1Θ©ΈΣΝΥΨΓΉν¥σΩ…Ρή‘ΎΗςΉ‘‘ –μΒΡ ±ΦδΡΎΗœΒΫ![]() ΒΊΘ§ΦΉΚΆ““”Π»γΚΈ―Γ‘ώΗςΉ‘ΒΡ¬ΖΨΕΘΩ
ΒΊΘ§ΦΉΚΆ““”Π»γΚΈ―Γ‘ώΗςΉ‘ΒΡ¬ΖΨΕΘΩ
Θ®2Θ©”Ο![]() ±μ ΨΦΉΓΔ““ΝΫ»Υ÷–‘Ύ‘ –μΒΡ ±ΦδΡΎΡήΗœΒΫ
±μ ΨΦΉΓΔ““ΝΫ»Υ÷–‘Ύ‘ –μΒΡ ±ΦδΡΎΡήΗœΒΫ![]() ΒΊΒΡ»Υ ΐΘ§’κΕ‘Θ®1Θ©ΒΡ―Γ‘ώΖΫΑΗΘ§«σ
ΒΊΒΡ»Υ ΐΘ§’κΕ‘Θ®1Θ©ΒΡ―Γ‘ώΖΫΑΗΘ§«σ![]() ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΓΘ
ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΓΘ
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦΉ”Π―Γ‘ώ![]() ,““”Π―Γ‘ώ
,““”Π―Γ‘ώ![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΒΡΖ÷≤ΦΝ–ΈΣ
ΒΡΖ÷≤ΦΝ–ΈΣ
X | 0 | 1 | 2 |
P | 0.04 | 0.42 | 0.54 |
![]() ΓΘ
ΓΘ
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©Ζ÷±πΦΤΥψΦΉΓΔ““ΝΫ»Υ―Γ‘ώΝΫ÷÷¬ΖΨΕ‘ΎΗςΉ‘‘ –μ ±ΦδΡΎΗœΒΫBΒΊΒΡΗ≈¬ Θ§±»ΫœΗ≈¬ ¥σ–ΓΦ¥Ω…Ής≥ω―Γ‘ώΘΜΘ®2Θ©”…Θ®1Θ©Ω…÷ΣΘ§ΦΉΓΔ““ΝΫ»Υ‘ΎΗςΉ‘‘ –μ ±ΦδΡΎΗœΒΫBΒΊΒΡΗ≈¬ ΈΣ![]() Ζ÷±πΦΤΥψΝΫ»ΥΖ≈«αΫ≈≤ΫΈ¥ΗœΒΫΓΔ÷Μ”–“Μ»ΥΗœΒΫΓΔΝΫ»ΥΕΦΗœΒΫΒΡΗ≈¬ Φ¥Ω…ΒΟΒΫΗ≈¬ Ζ÷≤ΦΝ–”κΤΎΆϊΓΘ
Ζ÷±πΦΤΥψΝΫ»ΥΖ≈«αΫ≈≤ΫΈ¥ΗœΒΫΓΔ÷Μ”–“Μ»ΥΗœΒΫΓΔΝΫ»ΥΕΦΗœΒΫΒΡΗ≈¬ Φ¥Ω…ΒΟΒΫΗ≈¬ Ζ÷≤ΦΝ–”κΤΎΆϊΓΘ
‘ΧβΫβΈωΘΚΘ®1Θ©”Ο![]() ±μ Ψ ¬ΦΰΓΑΦΉ―Γ‘ώ¬ΖΨΕ
±μ Ψ ¬ΦΰΓΑΦΉ―Γ‘ώ¬ΖΨΕ![]() ±Θ§40Ζ÷÷”ΡΎΗœΒΫ
±Θ§40Ζ÷÷”ΡΎΗœΒΫ![]() ΒΊΓ±Θ§
ΒΊΓ±Θ§![]() ±μ Ψ ¬ΦΰΓΑ““―Γ‘ώ¬ΖΨΕ
±μ Ψ ¬ΦΰΓΑ““―Γ‘ώ¬ΖΨΕ![]() ±Θ§50Ζ÷÷”ΡΎΗœΒΫ
±Θ§50Ζ÷÷”ΡΎΗœΒΫ![]() ΒΊΓ±Θ§
ΒΊΓ±Θ§![]() ΓΘ
ΓΘ
”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΦΑΤΒ¬ ΙάΦΤœύ”ΠΒΡΗ≈¬ Ω…ΒΟ
![]()
![]()
ΓΏ![]() Θ§Ι ΦΉ”Π―Γ‘ώ
Θ§Ι ΦΉ”Π―Γ‘ώ![]()
![]() Θ§
Θ§
![]() Θ§
Θ§
ΓΏ![]() Θ§Ι ““”Π―Γ‘ώ
Θ§Ι ““”Π―Γ‘ώ![]()
Θ®2Θ©”Ο![]() Ζ÷±π±μ Ψ’κΕ‘Θ®1Θ©ΒΡ―Γ‘ώΖΫΑΗΘ§ΦΉΓΔ““‘ΎΗςΉ‘‘ –μΒΡ ±ΦδΡΎΗœΒΫ
Ζ÷±π±μ Ψ’κΕ‘Θ®1Θ©ΒΡ―Γ‘ώΖΫΑΗΘ§ΦΉΓΔ““‘ΎΗςΉ‘‘ –μΒΡ ±ΦδΡΎΗœΒΫ![]() ΒΊΘ§
ΒΊΘ§
”…Θ®1Θ©÷Σ![]() Θ§
Θ§![]() Θ§”÷”…Χβ“β÷ΣΘ§
Θ§”÷”…Χβ“β÷ΣΘ§![]() œύΜΞΕάΝΔΘ§
œύΜΞΕάΝΔΘ§
Γύ![]()
![]()
![]()
![]()
Γύ![]() ΒΡΖ÷≤ΦΝ–ΈΣ
ΒΡΖ÷≤ΦΝ–ΈΣ
X | 0 | 1 | 2 |
P | 0.04 | 0.42 | 0.54 |
Γύ![]() ΓΘ
ΓΘ


 ÷«Ρή―ΒΝΖΝΖ≤βΩΦœΒΝ–¥πΑΗ
÷«Ρή―ΒΝΖΝΖ≤βΩΦœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΑ|x|ΘΦ2Γ± «ΓΑx2©¹x©¹6ΘΦ0Γ±ΒΡΘ® Θ©
A.≥δΖ÷Εχ≤Μ±Ί“ΣΧθΦΰ
B.±Ί“ΣΕχ≤Μ≥δΖ÷ΧθΦΰ
C.≥δ“ΣΧθΦΰ
D.Φ»≤Μ≥δΖ÷“≤≤Μ±Ί“ΣΧθΦΰ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΝΫΗω±δΝΩ÷°ΦδΒΡΙΊœΒ≤Μ «Κ· ΐΙΊœΒΒΡ «Θ® Θ©
A. ≥ωΉβ≥Β≥ΒΖ―”κ≥ωΉβ≥Β–– ΜΒΡάο≥Χ
B. …ΧΤΖΖΩœζ έΉήΦέ”κ…ΧΤΖΖΩΫ®÷ΰΟφΜΐ
C. ΧζΩιΒΡΧεΜΐ”κΧζΩιΒΡ÷ ΝΩ
D. »ΥΒΡ…μΗΏ”κΧε÷Ί
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ4Ηω≤ΜΆ§ΒΡ«ρΘ§4Ηω≤ΜΆ§ΒΡΚ–Ή”Θ§Α―«ρ»Ϊ≤ΩΖ≈»κΚ–ΡΎΘ°
Θ®1Θ©«Γ”–1ΗωΚ–≤ΜΖ≈«ρΘ§Ι≤”–ΦΗ÷÷Ζ≈Ζ®ΘΩ
Θ®2Θ©«Γ”–1ΗωΚ–ΡΎ”–2Ηω«ρΘ§Ι≤”–ΦΗ÷÷Ζ≈Ζ®ΘΩ
Θ®3Θ©«Γ”–2ΗωΚ–≤ΜΖ≈«ρΘ§Ι≤”–ΦΗ÷÷Ζ≈Ζ®ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥≥ßΦ“Ρβ‘Ύ2016ΡξΨΌ––¥ΌœζΜνΕ·Θ§Ψ≠Βς≤ι≤βΥψΘ§ΗΟ≤ζΤΖΒΡΡξœζ έΝΩΘ®Φ¥ΗΟ≥ßΒΡΡξ≤ζΝΩΘ©![]() ΆρΦΰ”κΡξ¥ΌœζΖ―”Ο
ΆρΦΰ”κΡξ¥ΌœζΖ―”Ο![]() Άρ‘ΣΘ®
Άρ‘ΣΘ®![]() Θ©¬ζΉψ
Θ©¬ζΉψ![]() ΈΣ≥Θ ΐ)Θ§»γΙϊ≤ΜΗψ¥ΌœζΜνΕ·Θ§‘ρΗΟ≤ζΤΖΒΡΡξœζ έ÷ΜΡή «
ΈΣ≥Θ ΐ)Θ§»γΙϊ≤ΜΗψ¥ΌœζΜνΕ·Θ§‘ρΗΟ≤ζΤΖΒΡΡξœζ έ÷ΜΡή «![]() ΆρΦΰ.“―÷Σ2016 Ρξ…ζ≤ζΗΟ≤ζΤΖΒΡΙΧΕ®ΆΕ»κΈΣ
ΆρΦΰ.“―÷Σ2016 Ρξ…ζ≤ζΗΟ≤ζΤΖΒΡΙΧΕ®ΆΕ»κΈΣ![]() Άρ‘Σ.ΟΩ…ζ≤ζ
Άρ‘Σ.ΟΩ…ζ≤ζ![]() ΆρΦΰΗΟ≤ζΤΖ–η“Σ‘ΌΆΕ»κ
ΆρΦΰΗΟ≤ζΤΖ–η“Σ‘ΌΆΕ»κ![]() Άρ‘ΣΘ§≥ßΦ“ΫΪΟΩΦΰ≤ζΤΖΒΡœζ έΦέΗώΕ®ΈΣΟΩΦΰ≤ζΤΖΡξΤΫΨυ≥…±ΨΒΡ
Άρ‘ΣΘ§≥ßΦ“ΫΪΟΩΦΰ≤ζΤΖΒΡœζ έΦέΗώΕ®ΈΣΟΩΦΰ≤ζΤΖΡξΤΫΨυ≥…±ΨΒΡ![]() ±ΕΘ®≤ζΤΖ≥…±ΨΑϋά®ΙΧΕ®ΆΕ»κΚΆ‘ΌΆΕ»κΝΫ≤ΩΖ÷Ή ΫπΘ©
±ΕΘ®≤ζΤΖ≥…±ΨΑϋά®ΙΧΕ®ΆΕ»κΚΆ‘ΌΆΕ»κΝΫ≤ΩΖ÷Ή ΫπΘ©
Θ®1Θ©ΫΪ2016 ΡξΗΟ≤ζΤΖΒΡάϊ»σ![]() Άρ‘Σ±μ ΨΈΣΡξ¥ΌœζΖ―”Ο
Άρ‘Σ±μ ΨΈΣΡξ¥ΌœζΖ―”Ο![]() Άρ‘ΣΒΡΚ· ΐΘΜ
Άρ‘ΣΒΡΚ· ΐΘΜ
Θ®2Θ©ΗΟ≥ßΦ“2016 ΡξΒΡ¥ΌœζΖ―”ΟΆΕ»κΕύ…ΌΆρ‘Σ ±Θ§≥ßΦ“ΒΡάϊ»σΉν¥σΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() ΓΘ
ΓΘ
Θ®1Θ©»τ«ζœΏ![]() ‘Ύ
‘Ύ![]() ¥ΠΒΡ«–œΏΖΫ≥ΧΈΣ
¥ΠΒΡ«–œΏΖΫ≥ΧΈΣ![]() Θ§«σ Β ΐ
Θ§«σ Β ΐ![]() ΚΆ
ΚΆ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©Χ÷¬έΚ· ΐ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
Θ®3Θ©»τ![]() Θ§«“Ε‘»Έ“β
Θ§«“Ε‘»Έ“β![]() Θ§ΕΦ”–
Θ§ΕΦ”–![]() Θ§«σ
Θ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() .
.
Θ®IΘ©Χ÷¬έ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
Θ®IIΘ©Β±![]() ”–Ήν¥σ÷Β,«“Ήν¥σ÷Β¥σ”Ύ
”–Ήν¥σ÷Β,«“Ήν¥σ÷Β¥σ”Ύ![]() ±,«σaΒΡ»Γ÷ΒΖΕΈß.
±,«σaΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΑΩΣΟ≈¥σΦΣΓ± «Ρ≥Βγ ”Χ®ΆΤ≥ωΒΡ”ΈœΖΫΎΡΩΓΘ―Γ ÷ΟφΕ‘![]() Κ≈8…»¥σΟ≈Θ§“ά¥ΈΑ¥œλΟ≈…œΒΡΟ≈ΝεΘ§
Κ≈8…»¥σΟ≈Θ§“ά¥ΈΑ¥œλΟ≈…œΒΡΟ≈ΝεΘ§
Ο≈ΝεΜα≤ΞΖ≈“ΜΕΈ“τά÷Θ®ΫΪ“Μ ΉΨ≠ΒδΝς––Ηη«ζ“‘ΒΞ“τ…Ϊ–ΐ¬…ΒΡΖΫ Ϋ―ί“οΘ©Θ§―Γ ÷–η’ΐ»Ζ¥π≥ω’β ΉΗηΒΡΟϊΉ÷Θ§
ΖΫΩ…ΜώΒΟΗΟ…»Ο≈Ε‘”ΠΒΡΦ“ΆΞΟΈœκΜυΫπΓΘ‘Ύ“Μ¥Έ≥ΓΆβΒς≤ι÷–Θ§ΖΔœ÷≤Έ»ϋ―Γ ÷¥σΕύ‘Ύ“‘œ¬ΝΫΗωΡξΝδΕΈΘΚ
![]() Θ§
Θ§![]() Θ®ΒΞΈΜΘΚΥξΘ©Θ§Ά≥ΦΤ’βΝΫΗωΡξΝδΕΈ―Γ ÷¥πΕ‘Ηη«ζΟϊ≥Τ”κΖώΒΡ»Υ ΐ»γœ¬ΆΦΥυ ΨΓΘ
Θ®ΒΞΈΜΘΚΥξΘ©Θ§Ά≥ΦΤ’βΝΫΗωΡξΝδΕΈ―Γ ÷¥πΕ‘Ηη«ζΟϊ≥Τ”κΖώΒΡ»Υ ΐ»γœ¬ΆΦΥυ ΨΓΘ

Θ®ΔώΘ©–¥≥ω![]() Ν–ΝΣ±μΘ§≤Δ≈–Εœ «Ζώ”–
Ν–ΝΣ±μΘ§≤Δ≈–Εœ «Ζώ”–![]() ΒΡΑ―Έ’»œΈΣ¥πΕ‘Ηη«ζΟϊ≥Τ”κΖώΚΆΡξΝδ”–ΙΊΘ§ΥΒΟςΡψΒΡάμ”…ΓΘΘ®œ¬
ΒΡΑ―Έ’»œΈΣ¥πΕ‘Ηη«ζΟϊ≥Τ”κΖώΚΆΡξΝδ”–ΙΊΘ§ΥΒΟςΡψΒΡάμ”…ΓΘΘ®œ¬
ΟφΒΡΝΌΫγ÷Β±μΙ©≤ΈΩΦΘ©
| 0.1 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
Θ®ΔρΘ©‘ΎΆ≥ΦΤΙΐΒΡ≤Έ»ϋ―Γ ÷÷–Α¥ΡξΝδΕΈΖ÷≤ψ―Γ»Γ9Οϊ―Γ ÷Θ§≤Δ≥ι»Γ3Οϊ–“‘Υ―Γ ÷Θ§«σ3Οϊ–“‘Υ―Γ ÷÷–‘Ύ
![]() ΥξΡξΝδΕΈΒΡ»Υ ΐΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΓΘ
ΥξΡξΝδΕΈΒΡ»Υ ΐΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΓΘ
Θ®≤ΈΩΦΙΪ ΫΘΚ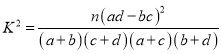 Θ§Τδ÷–
Θ§Τδ÷–![]() Θ©
Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΜßΆβ‘ΥΕ·“―Ψ≠≥…ΈΣ“Μ÷÷ ±…–‘ΥΕ·Θ§Ρ≥ΙΪΥΨΈΣΝΥΝΥΫβ‘±ΙΛœ≤ΜΕΜßΆβ‘ΥΕ· «Ζώ”κ–‘±π”–ΙΊΘ§ΨωΕ®¥”±ΨΙΪΥΨ»ΪΧε650»Υ÷–ΥφΜζ≥ι»Γ50»ΥΫχ––Έ ΨμΒς≤ιΓΘ
Θ®1Θ©Ά®ΙΐΕ‘Χτ―ΓΒΡ50»ΥΫχ––Βς≤ιΘ§ΒΟΒΫΝΥ»γœ¬![]() Ν–ΝΣ±μΘΚ
Ν–ΝΣ±μΘΚ
œ≤ΜΕΜßΆβ‘ΥΕ· | ≤Μœ≤ΜΕΜßΆβ‘ΥΕ· | ΚœΦΤ | |
Ρ–‘±ΙΛ | 5 | ||
≈°‘±ΙΛ | 10 | ||
ΚœΦΤ | 50 |
“―÷Σ‘Ύ’β50»Υ÷–ΥφΜζΧτ―Γ1»ΥΘ§¥Υ»Υœ≤ΜΕΜßΆβ‘ΥΕ·ΒΡΗ≈¬ «0.6Θ§«κΫΪ![]() Ν–ΝΣ±μ≤Ι≥δΆξ’ϊΘ§≤ΔΙάΦΤΗΟΙΪΥΨΡ–ΓΔ≈°‘±ΙΛΗςΕύ…Ό»ΥΘΜ
Ν–ΝΣ±μ≤Ι≥δΆξ’ϊΘ§≤ΔΙάΦΤΗΟΙΪΥΨΡ–ΓΔ≈°‘±ΙΛΗςΕύ…Ό»ΥΘΜ
Θ®2Θ©ΙάΦΤ”–Εύ¥σΒΡΑ―Έ’»œΈΣœ≤ΜΕΜßΆβ‘ΥΕ·”κ–‘±π”–ΙΊΘ§≤ΔΥΒΟςΡψΒΡάμ”…ΘΜ
Θ®3Θ©»τ”ΟΥφΜζ ΐ±μΖ®¥”650»Υ÷–≥ι»Γ‘±ΙΛΘ§œ÷ΙφΕ®¥”ΥφΜζ ΐ±μΘ®ΦϊΗΫ±μΘ©ΒΎ2––ΒΎ7Ν–ΒΡ ΐΩΣ ΦΆυ”“ΕΝΘ§‘ΎΉνœ»Χτ≥ωΒΡ5»Υ÷–Θ§»Έ»Γ2»ΥΘ§«σ»ΓΒΫΡ–‘±ΙΛ»Υ ΐΒΡ ΐ―ßΤΎΆϊΓΘ
ΗΫΘΚ
| 0.15 | 0Θ°10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
ΥφΜζ ΐ±μΘΚ
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com