
分析 ①,函数y=$\frac{1}{x}$的单调递减区间是(-∞,0),(0,+∞).
②,当n>0时,幂函数y=xn是(0,+∞)上的增函数.
③,函数y=ax2+1(a>1)的值域是[1,+∞).
④,当x>0,时,log2x2=2log2x才成立
⑤,根据轴对称的特征判定.
解答 解:对于①,函数y=$\frac{1}{x}$的单调递减区间是(-∞,0),(0,+∞),故错.
对于②,当n>0时,幂函数y=xn是(0,+∞)上的增函数,故错.
对于③,函数y=ax2+1(a>1)的值域是[1,+∞),故错.
对于④,当x>0,时,log2x2=2log2x才成立.故错
对于⑤,若函数y=f(x)满足f(1+x)=f(1-x),则函数f(x)的图象关于直线x=1对称.正确.
故答案为:⑤
点评 本题考查了命题真假的判定,涉及到了函数的概念及性质,属于基础题.


科目:高中数学 来源: 题型:解答题
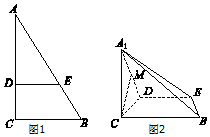 如图1,在Rt△ABC中,∠C=90°,BC=6,AC=9,D,E分别为AC、AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=6,AC=9,D,E分别为AC、AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$3 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com