
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为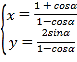 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),将曲线
),将曲线![]() 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的极坐标方程为
的极坐标方程为![]() ,普通方程为
,普通方程为![]() ;(2)
;(2)![]()
【解析】
(1)根据三角函数恒等变换可得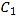 ,
, 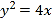 ,可得曲线
,可得曲线![]() 的普通方程,再运用图像的平移得依题意得曲线
的普通方程,再运用图像的平移得依题意得曲线![]() 的普通方程为,利用极坐标与平面直角坐标互化的公式可得方程;
的普通方程为,利用极坐标与平面直角坐标互化的公式可得方程;
(2)法一:将![]() 代入曲线
代入曲线![]() 的极坐标方程得
的极坐标方程得![]() ,运用韦达定理可得
,运用韦达定理可得![]() ,根据
,根据![]() ,可求得
,可求得![]() 的范围;
的范围;
法二:设直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线的倾斜角),代入曲线
为直线的倾斜角),代入曲线![]() 的普通方程得
的普通方程得![]() ,运用韦达定理可得
,运用韦达定理可得![]() ,根据
,根据![]() ,可求得
,可求得![]() 的范围;
的范围;
(1)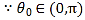 ,
, 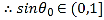
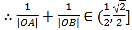 ,即曲线
,即曲线![]() 的普通方程为
的普通方程为![]() ,
,
依题意得曲线![]() 的普通方程为
的普通方程为![]() ,
,
令![]() ,
,![]() 得曲线
得曲线![]() 的极坐标方程为
的极坐标方程为![]() ;
;
(2)法一:将![]() 代入曲线
代入曲线![]() 的极坐标方程得
的极坐标方程得![]() ,则
,则
![]() ,
,![]() ,
,![]() ,
,![]() 异号
异号
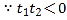 ,
,
![]() ,
,![]() ,
,![]() ;
;
法二:设直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线的倾斜角),代入曲线
为直线的倾斜角),代入曲线![]() 的普通方程得
的普通方程得![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() 异号
异号
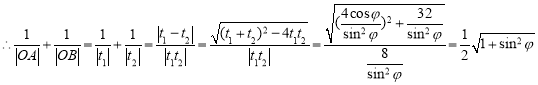
![]() ,
,![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 到点
到点![]() 的距离比它到
的距离比它到![]() 轴的距离多1,记点
轴的距离多1,记点![]() 的轨迹为
的轨迹为![]() ;
;
(1)求轨迹![]() 的方程;
的方程;
(2)求定点![]() 到轨迹
到轨迹![]() 上任意一点
上任意一点![]() 的距离
的距离![]() 的最小值;
的最小值;
(3)设斜率为![]() 的直线
的直线![]() 过定点
过定点![]() ,求直线
,求直线![]() 与轨迹
与轨迹![]() 恰好有一个公共点,两个公共点,三个公共点时
恰好有一个公共点,两个公共点,三个公共点时![]() 的相应取值范围.
的相应取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四位数的各位数字相加和为10,则称该数为“完美四位数”,如数字“2017”.试问用数字0,1,2,3,4,5,6,7组成的无重复数字且大于2017的“完美四位数”有( )个.
A. 71B. 66C. 59D. 53
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】半正多面体(semiregular solid) 亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形为面的半正多面体.如图所示,图中网格是边长为1的正方形,粗线部分是某二十四等边体的三视图,则该几何体的体积为( )
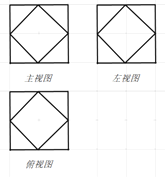
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农户考察三种不同的果树苗A、B、C,经引种试验后发现,引种树苗A的自然成活率为0.8,引种树苗B、C的自然成活率均为0.9.
(1)若引种树苗A、B、C各10棵.
①估计自然成活的总棵数;
②利用①的估计结论,从没有自然成活的树苗中随机抽取两棵,求抽到的两棵都是树苗A的概率;
(2)该农户决定引种B种树苗,引种后没有自然成活的树苗中有75%的树苗可经过人工栽培技术处理,处理后成活的概率为0.8,其余的树苗不能成活.若每棵树苗引种最终成活后可获利300元,不成活的每棵亏损50元,该农户为了获利不低于20万元,问至少引种B种树苗多少棵?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于统计数据的分析,有以下几个结论,其中正确的个数为( )
①利用残差进行回归分析时,若残差点比较均匀地落在宽度较窄的水平带状区域内,则说明线性回归模型的拟合精度较高;
②将一组数据中的每个数据都减去同一个数后,期望与方差均没有变化;
③调查剧院中观众观后感时,从50排(每排人数相同)中任意抽取一排的人进行调查是分层抽样法;
④已知随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作,书中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”,该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚减一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数![]() 是8的整数倍时,均可采用此方法求解,如图是解决这类问题的程序框图,若输入
是8的整数倍时,均可采用此方法求解,如图是解决这类问题的程序框图,若输入![]() ,则输出的结果为( )
,则输出的结果为( )
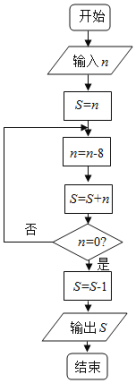
A.80B.47C.79D.48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中真命题的个数是![]()
![]()
![]() 中,
中,![]() 是
是![]() 的三内角A,B,C成等差数列的充要条件;
的三内角A,B,C成等差数列的充要条件;
![]() 若“
若“![]() ,则
,则![]() ”的逆命题为真命题;
”的逆命题为真命题;
![]() 是
是![]() 或
或![]() 充分不必要条件;
充分不必要条件;
![]() 是
是![]() 的充要条件.
的充要条件.
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com