在等差数列

中,

,

则
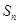
的最大值为____________.
试题分析:由

得,
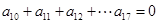
,即
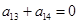
,又因为

,所以
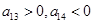
,且
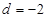
,当

时
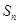
取得最大值,最大值为

.
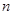
项和.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知数列
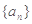
前n项和为
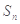
,首项为
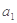
,且
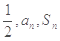
成等差数列.
(1)求数列
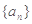
的通项公式;
(2)数列满足
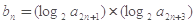
,求证:
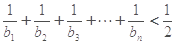
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知等差数列
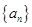
满足:
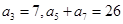
.
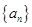
的前
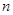
项和为
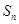 。
。(Ⅰ)求
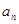
及
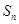
;
(Ⅱ)令
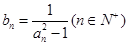
,求数列
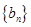
的前
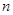
项和
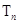
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设
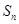
为数列
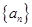
的前
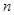
项和,且有
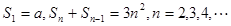
(Ⅰ)求数列
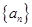
的通项公式;
(Ⅱ)若数列
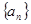
是单调递增数列,求
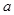
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设数列
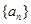
的前
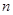
项和为

,且

.
(1)求数列
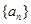
的通项公式;
(2)设

求证:

.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
在等差数列
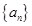
,等比数列
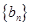
中,
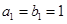
,
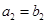
,
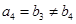
.
(1)求
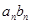
;
(2)设
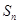
为数列
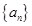
的前
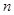
项和,
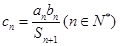
,
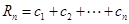
,求
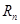
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知数列
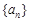
的首项
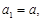
其中
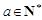
,
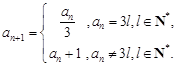
,令集合
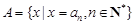
.
(1)若
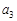
是数列
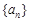
中首次为1的项,请写出所有这样数列的前三项;
(2)求证:对
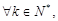
恒有
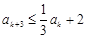
成立;
(3)求证:
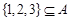
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在等差数列
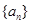
中,已知

,则该数列前11项的和
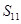
等于( )
查看答案和解析>>

 期末集结号系列答案
期末集结号系列答案