
【题目】已知函数![]() .
.
(1)判断![]() 的单调性;
的单调性;
(2)若![]() 在(1,+∞)上恒成立,且
在(1,+∞)上恒成立,且![]() =0有唯一解,试证明a<1.
=0有唯一解,试证明a<1.
【答案】(1)f(x)在(0,![]() )递减,在(
)递减,在(![]() ,+∞)递增;(2)见解析
,+∞)递增;(2)见解析
【解析】
(1)求出函数的导数,解关于导函数的方程,求出函数的单调区间即可;
(2)问题转化为﹣2lnx0![]() 0,令g(x0)=﹣2lnx0
0,令g(x0)=﹣2lnx0![]() ,根据函数的单调性证明即可.
,根据函数的单调性证明即可.
(1)函数的定义域是(0,+∞),
f′(x)![]() x﹣a
x﹣a![]() ,
,
易知x2﹣ax﹣2=0有两根,x1![]() 0,x2
0,x2![]() ,
,
故f(x)在(0,![]() )递减,在(
)递减,在(![]() ,+∞)递增;
,+∞)递增;
(2)∵a<0,∴![]() 1,
1,
∴f′(x)在(1,+∞)上有唯一零点x0![]() ,
,
又f′(x)![]() x﹣a,∴
x﹣a,∴![]() x0﹣a=0①,
x0﹣a=0①,
要使f(x)≥0在区间(1,+∞)恒成立,且f(x)=0有唯一解,
须f(x0)=0,即﹣2lnx0![]() (
(![]() 1)﹣ax0=0②,
1)﹣ax0=0②,
由①②得:
﹣2lnx0![]() (
(![]() 1)﹣x0(
1)﹣x0(![]() x0)=0,
x0)=0,
故﹣2lnx0![]() 0,
0,
令g(x0)=﹣2lnx0![]() ,
,
显然g(x0)在(1,+∞)递减,
∵g(1)=2>0,g(2)=﹣2ln2![]() 0,
0,
∴1<x0<2,
又∵a![]() x0在(1,+∞)递增,
x0在(1,+∞)递增,
故a<1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某生产基地有五台机器,现有五项工作待完成,每台机器完成每项工作后获得的效益值如表所示.若每台机器只完成一项工作,且完成五项工作后获得的效益值总和最大,则下列叙述错误的的是_____________.
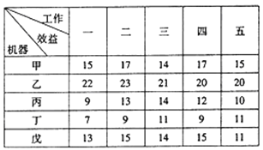
①甲只能承担第四项工作
②乙不能承担第二项工作
③丙可以不承担第三项工作
④丁可以承担第三项工作
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 、
、![]() 为大于3的整数,将
为大于3的整数,将![]() 的立方体分割为
的立方体分割为![]() 个单位正方体,从一角的单位正方体起第
个单位正方体,从一角的单位正方体起第![]() 层、第
层、第![]() 行、第
行、第![]() 列的单位正方体记为
列的单位正方体记为![]() .求所有有序六元数组
.求所有有序六元数组![]() 的个数,使得一只蚂蚁从
的个数,使得一只蚂蚁从![]() 出发,经过每个小正方体恰一次到达
出发,经过每个小正方体恰一次到达![]() .(注)蚂蚁可以从一个单位正方体爬到另一个与之有公共面的相邻正方体.
.(注)蚂蚁可以从一个单位正方体爬到另一个与之有公共面的相邻正方体.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农历戊戌年即将结束,为了迎接新年,小康、小梁、小谭、小刘、小林每人写了一张心愿卡,设计了一个与此心愿卡对应的漂流瓶.现每人随机的选择一个漂流瓶将心愿卡放入,则事件“至少有两张心愿卡放入对应的漂流瓶”的概率为___
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,且
是正方形,且![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的一个动点.
上的一个动点.
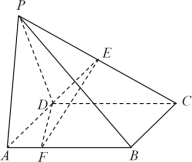
(Ⅰ)求证:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)设二面角![]() 的平面角为
的平面角为![]() ,试判断在线段
,试判断在线段![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com