
| A. | 充分必要条件 | B. | 充分条件但非必要条件 | ||
| C. | 必要条件但非充分条件 | D. | 既非充分条件又非必要条件 |
分析 由f(0)=0可得$\underset{lim}{x→0}$$\frac{F(x)-F(0)}{x}$=$\underset{lim}{x→0}$$\frac{f(x)(1+|sinx|)}{x}$=$\underset{lim}{x→0}$$\frac{f(x)}{x}$=f′(0);
若F(x)在x=0处可导,当x在0的左侧附近时,F′(x)=f′(x)(1-sinx)-f(x)cosx,当x在0的右侧附近时,F′(x)=f′(x)(1+sinx)+f(x)cosx,从而可得$\underset{lim}{x→{0}^{-}}$$\frac{F(x)-F(0)}{x}$=f′(0)-f(0),$\underset{lim}{x→{0}^{+}}$$\frac{F(x)-F(0)}{x}$=f′(0)+f(0),从而可得f′(0)-f(0)=f′(0)+f(0),从而解得.
解答 解:∵f(0)=0,
∴$\underset{lim}{x→0}$$\frac{F(x)-F(0)}{x}$
=$\underset{lim}{x→0}$$\frac{f(x)(1+|sinx|)}{x}$
=$\underset{lim}{x→0}$$\frac{f(x)}{x}$=f′(0),
故F(x)在x=0处可导;
若F(x)在x=0处可导,
当x在0的左侧附近时,
F(x)=f(x)(1-sinx),
F′(x)=f′(x)(1-sinx)-f(x)cosx,
当x在0的右侧附近时,
F(x)=f(x)(1+sinx),
F′(x)=f′(x)(1+sinx)+f(x)cosx,
故$\underset{lim}{x→{0}^{-}}$$\frac{F(x)-F(0)}{x}$=f′(0)-f(0),
$\underset{lim}{x→{0}^{+}}$$\frac{F(x)-F(0)}{x}$=f′(0)+f(0),
∴f′(0)-f(0)=f′(0)+f(0),
∴f(0)=0;
故选:A.
点评 本题考查了导数的概念及左右极限的应用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
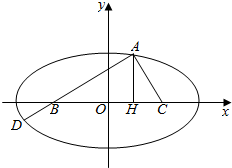 如图,B(-c,0),C(c,0),AH⊥BC,垂足为H,且$\overrightarrow{BH}$=3$\overrightarrow{HC}$.又$\overrightarrow{AD}$=-4$\overrightarrow{DB}$,且A、D同在B、C为焦点的椭圆上,求椭圆的离心率.
如图,B(-c,0),C(c,0),AH⊥BC,垂足为H,且$\overrightarrow{BH}$=3$\overrightarrow{HC}$.又$\overrightarrow{AD}$=-4$\overrightarrow{DB}$,且A、D同在B、C为焦点的椭圆上,求椭圆的离心率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
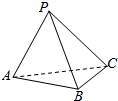
| A. | AP⊥PB,AP⊥PC | B. | AP⊥PB,BC⊥PB | ||
| C. | 平面BPC⊥平面APC,BC⊥PC | D. | AP⊥平面PBC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com