
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |
| bc | ||
|
| a•PD | ||
|
| a2b2c2 |
| a2b2+b2c2+c2a2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
| 1 |
| h2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
| 1 |
| h2 |


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
在平面几何中有:Rt△ABC的直角边分别为a,b,斜边上的高为h,则![]() .类比这一结论,在三棱锥P―ABC中,PA、PB、PC两两互相垂直,且PA=a,PB=b,PC=c,此三棱锥P―ABC的高为h,则结论为______________
.类比这一结论,在三棱锥P―ABC中,PA、PB、PC两两互相垂直,且PA=a,PB=b,PC=c,此三棱锥P―ABC的高为h,则结论为______________
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年河南省郑州外国语学校高二下学期期中考试数学卷(文) 题型:填空题
在平面几何中有:Rt△ABC的直角边分别为a,b,斜边上的高为h,则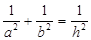 .类比这一结论,在三棱锥P—ABC中,PA、PB、PC两两互相垂直,且PA=a,PB=b,PC=c,此三棱锥P—ABC的高为h,则结论为______________
.类比这一结论,在三棱锥P—ABC中,PA、PB、PC两两互相垂直,且PA=a,PB=b,PC=c,此三棱锥P—ABC的高为h,则结论为______________
查看答案和解析>>
科目:高中数学 来源:2010届高三数学每周精析精练:选考部分 题型:填空题
在平面几何中有:Rt△ABC的直角边分别为a,b,斜边上的高为h,则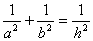 .类比这一结论,在三棱锥P—ABC中,PA、PB、PC两两互相垂直,且PA=a,PB=b,PC=c,此三棱锥P—ABC的高为h,则结论为______________
.类比这一结论,在三棱锥P—ABC中,PA、PB、PC两两互相垂直,且PA=a,PB=b,PC=c,此三棱锥P—ABC的高为h,则结论为______________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com