
【题目】已知函数![]() ,其中
,其中![]() ,且函数
,且函数![]() 的最小正周期为
的最小正周期为![]() 。
。
(1)若函数![]() 在
在![]() 处取到最小值
处取到最小值![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)若将函数![]() 图象上所有点的横坐标伸长到原来的
图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),再将向左平移
倍(纵坐标不变),再将向左平移![]() 个单位,得到的函数图象关于
个单位,得到的函数图象关于![]() 轴对称,求函数
轴对称,求函数![]() 的单调递增区间。
的单调递增区间。
科目:高中数学 来源: 题型:
【题目】下面是某市环保局连续30天对空气质量指数的监测数据:
61 76 70 56 81 91 55 91 75 81
88 67 101 103 57 91 77 86 81 83
82 82 64 79 86 85 75 71 49 45
(Ⅰ)完成下面的频率分布表;
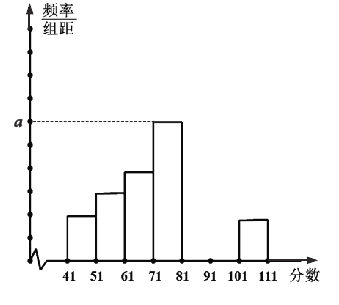
(Ⅱ)完成下面的频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;
(Ⅲ)在本月空气质量指数大于等于91的这些天中随机选取两天,求这两天中至少有一天空气质量指数在区间![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求![]() 的展开式中
的展开式中![]() 的系数及展开式中各项系数之和;
的系数及展开式中各项系数之和;
(2)从0,2,3,4,5,6这6个数字中任取4个组成一个无重复数字的四位数,求满足条件的四位数的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,函数
,函数![]() ,若函数
,若函数![]() 的图象与
的图象与![]() 轴的两个相邻交点的距离为
轴的两个相邻交点的距离为![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() 时,
时, ![]() ,求
,求![]() 的值.
的值.
(3)若![]() ,且
,且![]() 有且仅有一个实根,求实数
有且仅有一个实根,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级某次数学竞赛随机抽取![]() 名学生的成绩,分组为
名学生的成绩,分组为![]() ,统计后得到频率分布直方图如图所示:
,统计后得到频率分布直方图如图所示:
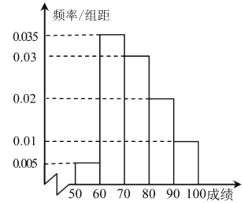
(1)试估计这组样本数据的众数和中位数(结果精确到![]() );
);
(2)年级决定在成绩![]() 中用分层抽样抽取
中用分层抽样抽取![]() 人组成一个调研小组,对髙一年级学生课外学习数学的情况做一个调查,则在
人组成一个调研小组,对髙一年级学生课外学习数学的情况做一个调查,则在![]() 这三组分別抽取了多少人?
这三组分別抽取了多少人?
(3)现在要从(2)中抽取的![]() 人中选出正副
人中选出正副![]() 个小组长,求成绩在
个小组长,求成绩在![]() 中至少有
中至少有![]() 人当选为正、副小组长的概率.
人当选为正、副小组长的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() ,其中
,其中![]() .
.
(1)设![]() ,证明:数列
,证明:数列![]() 是等差数列;
是等差数列;
(2)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() ;
;
(3)设![]() (
(![]() 为非零整数,
为非零整数,![]() ),试确定
),试确定![]() 的值,使得对任意
的值,使得对任意![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“开门大吉”是某电视台推出的游戏益智节目.选手面对![]() 号
号![]() 扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:
扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:![]() ;
;![]() (单位:岁),其猜对歌曲名称与否人数如图所示.
(单位:岁),其猜对歌曲名称与否人数如图所示.
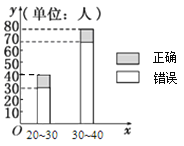
(1)写出![]() 列联表:判断是否有
列联表:判断是否有![]() 的把握认为猜对歌曲名称与否与年龄有关?
的把握认为猜对歌曲名称与否与年龄有关?
说明你的理由.(下面的临界值表供参考)

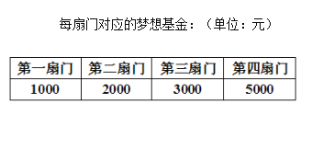
(2)若某选手能正确回答第一、二、三、四扇门的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,正确回答一个问题后,选择继续回答下一个问题的概率是
,正确回答一个问题后,选择继续回答下一个问题的概率是![]() ,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为
,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
(参考公式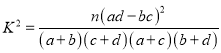 其中
其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com