
【题目】下列命题中错误的是![]()
![]()
A. 若命题![]() 为真命题, 命题
为真命题, 命题![]() 为假命题, 则命题“
为假命题, 则命题“![]() ”为真命题
”为真命题
B. 命题“若![]() ,则
,则![]() 或
或![]() ”为真命题
”为真命题
C. 对于命题![]() ,
,![]() ,则
,则![]() ,
,![]()
D. “![]() ”是“
”是“![]() ”的充分不必要条件个
”的充分不必要条件个
【答案】D
【解析】
由复合命题的真值表即可判断A;由原命题的逆否命题的真假,可判断B;
由全称命题的否定为特称命题,可判断C;由二次方程的解法,结合充分必要条件的定义可判断D.
若命题p为真命题,命题q为假命题,则¬q为真命题,
命题“p∨(¬q)”为真命题,故A正确;
命题“若x+y≠5,则x≠2或y≠3”的逆否命题为“若x=2且y=3,则x+y=5”为真命题,
可得原命题为真命题,故B正确;
命题p:x∈R,x2+x+1>0,则¬p:x0∈R,x02+x0+1≤0,故C正确;
“x=1”可推得“x2﹣3x+2=0”,反之不成立,
“x2﹣3x+2=0”是“x=1”的必要不充分条件,故D错误.
故选:D.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠DAB=60°.
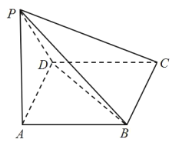
(1)证明:AD⊥PB.
(2)若PB=![]() ,AB=PA=2,求三棱锥P-BCD的体积。
,AB=PA=2,求三棱锥P-BCD的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
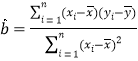
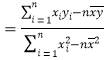 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() (a>0,b>0)的渐近线方程为y=±
(a>0,b>0)的渐近线方程为y=±![]() x,右顶点为(1,0).
x,右顶点为(1,0).
(1)求双曲线C的方程;
(2)已知直线y=x+m与双曲线C交于不同的两点A,B,且线段AB的中点为![]() ,当x0≠0时,求
,当x0≠0时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知高中学生的数学成绩与物理成绩具有线性相关关系,在一次考试中某班7名学生的数学成绩与物理成绩如下表:
数学成绩 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理成绩 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)求这7名学生的数学成绩的极差和物理成绩的平均数;
(2)求物理成绩![]() 对数学成绩
对数学成绩![]() 的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
下列公式与数据可供参考:
用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
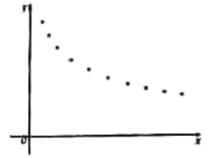
【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图).
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图).
|
|
|
|
|
|
|
1.63 | 37.8 | 0.89 | 5.15 | 0.92 |
| 18.40 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适合作价格
哪一个更适合作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程.
的回归方程.
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() ,求该产品投放市场第几天的销售额最高?最高为多少元?
,求该产品投放市场第几天的销售额最高?最高为多少元?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为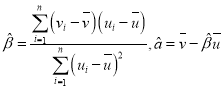 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com