
分析 (Ⅰ)求出函数的导数,计算f(3),f′(3)的值,求出切线方程即可;
(Ⅱ)求出函数f(x)的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅲ)由(Ⅱ)知x0处有极值,求出${x_0}=1+\sqrt{a+1}$,得到f(x)在[e+2,e3+2]上单调,根据函数的单调性得到关于a的不等式组,解出即可.
解答 解:$f'(x)=\frac{1}{x-2}-\frac{x}{a}$(x>2)
(Ⅰ)当a=1时,$f'(x)=\frac{1}{x-2}x$,f'(3)=-2.$f(3)=-\frac{9}{2}$,
所以,函数f(x)在点(3,f(3))处的切线方程为:
$y+\frac{9}{2}=-2({x-3})$,即4x+2y-3=0.…(3分)
(Ⅱ)$f'(x)=\frac{1}{x-2}-\frac{x}{a}=-\frac{{{x^2}-2x-a}}{{a({x-2})}}$=$-\frac{1}{{a({x-2})}}[{{{({x-1})}^2}-({a+1})}]$,
因为x>2,所以x-2>0,
①当a<0时,(x-1)2-(a+1)=x(x-2)-a>0在x>2上成立,
所以f'(x)当x>2恒大于0,
故f(x)在(2,+∞)上是增函数.…(5分)
②当a>0时,$f'(x)=-\frac{1}{{a({x-2})}}({x-1+\sqrt{a+1}})({x-1-\sqrt{a+1}})$,
因为x>2,
所以$x-1+\sqrt{a+1}>0$,a(x-2)>0,
当$x≥1+\sqrt{a+1}$时,f'(x)≤0,f(x)为减函数;
当$2≤x≤1+\sqrt{a+1}$时,f'(x)≥0,f(x)为增函数.…(7分)
综上:当a<0时,f(x)在(2,+∞)上为增函数;
当a>0时,f(x)在$({2,1+\sqrt{a+1}})$上为增函数,在$({1+\sqrt{a+1},+∞})$上为减函数.…(8分)
(Ⅲ)由(Ⅱ)知x0处有极值,故a>0,且${x_0}=1+\sqrt{a+1}$,
因为${x_0}∉[{e+2,{e^3}+2}]$且e+2>2,
所以f(x)在[e+2,e3+2]上单调.…(10分)
当[e+2,e3+2]为增区间时,f(x)≥0恒成立,则有$\left\{\begin{array}{l}{e^3}+2<1+\sqrt{a+1}\\ f({e+2})≥0\end{array}\right.⇒a>{e^6}+2{e^3}$.
当[e+2,e3+2]为减区间时,f(x)≥0恒成立,则有$\left\{\begin{array}{l}e+2>1+\sqrt{a+1}\\ f({{e^3}+2})≥0\end{array}\right.⇒\left\{\begin{array}{l}a<{e^2}+2e\\ a≥\frac{{{e^6}+4{e^3}+4}}{6}\end{array}\right.$解集为空集.
综上:当a>e6+2e3时满足条件.…(12分)
点评 本题考查了切线方程问题,考查函数的单调性问题,考查导数的应用以及分类讨论思想,是一道综合题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
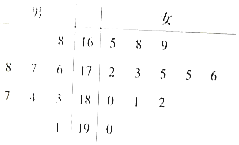 某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
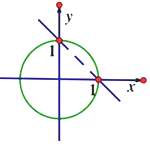
| A. | (x+y-1)•(x2+y2-1)=0 | B. | $\sqrt{x+y-1}•({x^2}+{y^2}-1)=0$ | ||
| C. | $(x+y-1)•\sqrt{{x^2}+{y^2}-1}=0$ | D. | $\sqrt{x+y-1}•\sqrt{{x^2}+{y^2}-1}=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com