
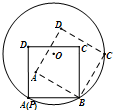
 设圆O的半径为2,点P为圆周上给定一点,如图所示,放置边长为2的正方形ABCD(实线所示,正方形的顶点A与点P重合,点B在圆周上).现将正方形ABCD沿圆周按顺时针方向连续滚动,当点A首次回到点P的位置时,点A所走过的路径的长度为( )
设圆O的半径为2,点P为圆周上给定一点,如图所示,放置边长为2的正方形ABCD(实线所示,正方形的顶点A与点P重合,点B在圆周上).现将正方形ABCD沿圆周按顺时针方向连续滚动,当点A首次回到点P的位置时,点A所走过的路径的长度为( )| A、4π | ||||
B、(3+
| ||||
C、(1+2
| ||||
D、(2+
|
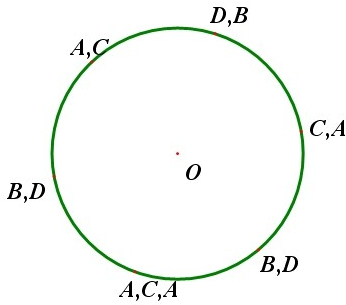 ∵圆O的半径r=2,正方形ABCD的边长a=2,
∵圆O的半径r=2,正方形ABCD的边长a=2,| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
2
| ||
| 6 |
| π |
| 6 |
| π |
| 3 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
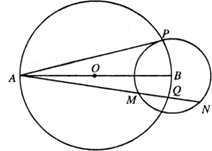
 (2012•河南模拟)如图,AB是圆O的直径,以B为圆心的圆B与圆O的一个交点为P.过点A作直线交圆O于点Q,交圆B于点M、N.
(2012•河南模拟)如图,AB是圆O的直径,以B为圆心的圆B与圆O的一个交点为P.过点A作直线交圆O于点Q,交圆B于点M、N.| 10 | 3 |
查看答案和解析>>
科目:高中数学 来源:河北省正定中学2011-2012学年高二下学期第二次考试数学文科试题 题型:044
如图,AB是圆O的直径,以B为圆心的圆B与圆O的一个交点为P.过点A作直线交圆O于点Q,交圆B于点M、N.
(Ⅰ)求证:QM=QN;
(Ⅱ)设圆O的半径为2,圆B的半径为1,当![]() 时,求MN的长.
时,求MN的长.
查看答案和解析>>
科目:高中数学 来源:2012届度河北省唐山市高三年级第一次模拟考试数学试卷 题型:解答题
选修4-1:几何证明选讲
如图,AB是圆O的直径,以B为圆心的圆B与圆O的一个交点为P.过点A作直线交圆O于点Q,交圆B于点M、N.
(I )求证:QM=QN;
(II)设圆O的半径为2,圆B的半径为1,当AM= 时,求MN的长.
时,求MN的长.

查看答案和解析>>
科目:高中数学 来源:2012年山西省运城市康杰中学高考数学模拟试卷1(文科)(解析版) 题型:解答题
 时,求MN的长.
时,求MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com