
分析 根据三角形的重心公式与性质,得出向量$\overrightarrow{AD}$=3$\overrightarrow{MD}$,利用坐标表示,即可求出重心坐标.
解答 解:△ABC中,A(3,1),BC的中点为D(-3,1),
设重心M的坐标为(x,y),
则$\overrightarrow{AD}$=3$\overrightarrow{MD}$,
即(-3-3,1-1)=3(-3-x,1-y),
∴$\left\{\begin{array}{l}{-6=3(-3-x)}\\{0=3(1-y)}\end{array}\right.$),
解得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$;
∴△ABC的重心M的坐标为(-1,1).
故答案为:(-1,1).
点评 本题考查了平面向量的坐标运算问题,也考查了三角形的重心公式与性质的应用问题,是基础题目.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
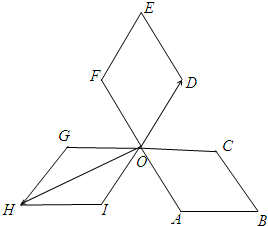 如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( )
如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,+∞) | B. | (-∞,-1) | C. | (-∞,1) | D. | (-∞,-1)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com