练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的中心在坐标原点，焦点在轴上且过点，离心率是.

    （1）求椭圆的标准方程；

    （2）直线过点且与椭圆交于两点，若，求直线的方程.

    【答案】（1）＋y2＝1（2）x＋6y＋＝0和x－6y＋＝0.

    【解析】试题分析：（1）由题设条件知关于a,b,c的方程组，由此能求出椭圆方程．

    （2）可以设直线方程（斜率不存在单独考虑），然后与椭圆方程联立，消去y得到关于x的一元二次方程，利用韦达定理结合题目条件建立方程即可求出直线方程.

    试题解析：（1）设椭圆的方程为.

    由已知可得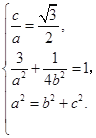3分

    解得， .

    故椭圆的方程为． 6分

    （2）由已知，若直线的斜率不存在，则过点的直线的方程为，

    此时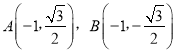，显然不成立． 7分

    若直线的斜率存在，则设直线的方程为．

    则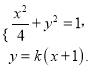

    整理得． 9分

    由

    ．

    设．

    故，①． ② 10分

    因为，即．③

    ①②③联立解得． 13分

    所以直线的方程为和． 14分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了研究“教学方式”对教学质量的影响，某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学（勤奋程度和自觉性都一样）．如图茎叶图为甲、乙两班（每班均为20人）学生的数学期末考试成绩．

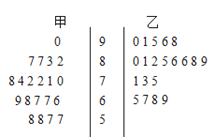
    （1）现从甲班数学成绩不低于80分的同学中随机抽取两名同学，求成绩为87分的同学至少有一名被抽中的概率；

    （2）学校规定：成绩不低于75分的为优秀，请填写列联表，并判断有多大把握认为“成绩优秀与教学方式有关”．

    甲班

    乙班

    合计

    优秀

    不优秀

    合计

    参考公式与临界值表： ．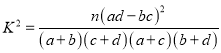

    0.100

    0.050

    0.025

    0.010

    0.001

    2.706

    3.841

    5.024

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4—5: 不等式选讲

    已知函数f(x)＝ 的定义域为R.

    (Ⅰ)求实数m的取值范围；

    (Ⅱ)若m的最大值为n，当正数a，b满足 ＝n时，求7a＋4b的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （Ⅰ）求的值．

    （Ⅱ）求函数在区间上的最大值和最小值，及相应的的值．

    （Ⅲ）求函数在区间的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）已知函数．

    （1）求函数的最小正周期和单调递增区间；

    （2）若在中，角，，的对边分别为，，，，为锐角，且，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，侧棱底面， 为棱中点． ， ， ．

    （I）求证： 平面．

    （II）求证： 平面．

    （III）在棱的上是否存在点，使得平面平面？如果存在，求此时的值；如果不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市拟兴建九座高架桥，新闻媒体对此进行了问卷调查，在所有参与调查的市民中，持“支持”、“保留”和“不支持”态度的人数如下表所示：

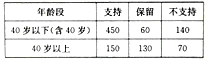
    （1）在所有参与调查的人中，用分层抽样的方法抽取部分市民做进一步调研（不同态度的群体中亦按年龄分层抽样），已知从“保留”态度的人中抽取了19人，则在“支持”态度的群体中，年龄在40岁以下（含40岁）的人有多少被抽取；

    （2）在持“不支持”态度的人中，用分层抽样的方法抽取6人做进一步的调研，将此6人看作一个总体，在这6人中任意选取2人，求至少有1人在40岁以上的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆： 的离心率为，过其右焦点与长轴垂直的直线与椭圆在第一象限相交于点， .

    （1）求椭圆的标准方程；

    （2）设椭圆的左顶点为，右顶点为，点是椭圆上的动点，且点与点， 不重合，直线与直线相交于点，直线与直线相交于点，求证：以线段为直径的圆恒过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： （）的离心率为，右焦点为，斜率为1的直线与椭圆交于、两点，以为底边作等腰三角形，顶点为．

    （1）求椭圆的方程；

    （2）求△的面积．

    查看答案和解析>>

    同步练习册答案