
ЎҫМвДҝЎҝТСЦӘПВБРГьМвЈә
ўЩГьМвЎ°![]() Ј¬
Ј¬ ![]() ЎұөД·с¶ЁКЗЈәЎ°
ЎұөД·с¶ЁКЗЈәЎ°![]() Ј¬
Ј¬ ![]() ЎұЈ»
ЎұЈ»
ўЪИфСщұҫКэҫЭ![]() өДЖҪҫщЦөәН·ҪІо·ЦұрОӘ
өДЖҪҫщЦөәН·ҪІо·ЦұрОӘ![]() әН
әН![]() ФтКэҫЭ
ФтКэҫЭ![]() өДЖҪҫщЦөәНұкЧјІо·ЦұрОӘ
өДЖҪҫщЦөәНұкЧјІо·ЦұрОӘ![]() Ј¬
Ј¬ ![]() Ј»
Ј»
ўЫБҪёцКВјюІ»КЗ»ҘівКВјюөДұШТӘІ»ід·ЦМхјюКЗБҪёцКВјюІ»КЗ¶ФБўКВјюЈ»
ўЬФЪ![]() БРБӘұнЦРЈ¬ИфұИЦө
БРБӘұнЦРЈ¬ИфұИЦө![]() Ул
Ул![]() ПаІоФҪҙуЈ¬ФтБҪёц·ЦАаұдБҝУР№ШПөөДҝЙДЬРФҫНФҪҙуЈ®
ПаІоФҪҙуЈ¬ФтБҪёц·ЦАаұдБҝУР№ШПөөДҝЙДЬРФҫНФҪҙуЈ®
ўЭТСЦӘ![]() ОӘБҪёцЖҪГжЈ¬ЗТ
ОӘБҪёцЖҪГжЈ¬ЗТ![]() Ј¬
Ј¬ ![]() ОӘЦұПЯЈ®ФтГьМв:Ў°Иф
ОӘЦұПЯЈ®ФтГьМв:Ў°Иф![]() Ј¬Фт
Ј¬Фт![]() ЎұөДДжГьМвәН·сГьМвҫщОӘјЩГьМвЈ®
ЎұөДДжГьМвәН·сГьМвҫщОӘјЩГьМвЈ®
ўЮЙи¶Ёөг![]() Ўў
Ўў![]() Ј¬¶Ҝөг
Ј¬¶Ҝөг![]() ВъЧгМхјю
ВъЧгМхјю![]() ОӘХэіЈКэЈ©Ј¬Фт
ОӘХэіЈКэЈ©Ј¬Фт![]() өД№мјЈКЗНЦФІЈ®ЖдЦРХжГьМвөДёцКэОӘ( )
өД№мјЈКЗНЦФІЈ®ЖдЦРХжГьМвөДёцКэОӘ( )
A. 5 B. 4 C. 3 D. 2
Ўҫҙр°ёЎҝA
ЎҫҪвОцЎҝўЩГьМвЎ°![]() Ј¬
Ј¬ ![]() ЎұөД·с¶ЁКЗЈәЎ°
ЎұөД·с¶ЁКЗЈәЎ°![]() Ј¬
Ј¬ ![]() Ўұ,ГьМвХэИ·;
Ўұ,ГьМвХэИ·;
ўЪКэҫЭ![]() өДұкЧјІо
өДұкЧјІо![]() Ј¬ЖҪҫщКэОӘЈә
Ј¬ЖҪҫщКэОӘЈә ![]() Ј¬
Ј¬
ГьМвХэИ·Ј»
ўЫЖдДж·сГьМвКЗЈәБҪКВјюКЗ¶ФБўКВјюөДұШТӘІ»ід·ЦМхјюКЗБҪёцКВјюКЗ»ҘівКВјю.ГьМвХэИ·Ј»
ўЬ![]() ©Ғ
©Ғ![]() =
=![]() Ј¬ЎЯad©ҒbcПаІоФҪҙуЈ¬БҪёц·ЦАаұдБҝУР№ШПөөДҝЙДЬРФҫНФҪҙуЈ¬
Ј¬ЎЯad©ҒbcПаІоФҪҙуЈ¬БҪёц·ЦАаұдБҝУР№ШПөөДҝЙДЬРФҫНФҪҙуЈ¬
Ўа![]() ©Ғ
©Ғ![]() =ПаІоФҪҙуЈ¬БҪёц·ЦАаұдБҝУР№ШПөөДҝЙДЬРФҫНФҪҙуЈ¬ГьМвХэИ·Ј»
=ПаІоФҪҙуЈ¬БҪёц·ЦАаұдБҝУР№ШПөөДҝЙДЬРФҫНФҪҙуЈ¬ГьМвХэИ·Ј»
ўЭДжГьМвЈәТСЦӘ![]() ОӘБҪёцЖҪГжЈ¬ЗТ
ОӘБҪёцЖҪГжЈ¬ЗТ![]() Ј¬
Ј¬ ![]() ОӘЦұПЯЈ®ФтГьМв:Ў°Иф
ОӘЦұПЯЈ®ФтГьМв:Ў°Иф![]() Ј¬Фт
Ј¬Фт![]() ЎұПФИ»lУлЖҪГж
ЎұПФИ»lУлЖҪГж![]() №ШПөІ»И·¶ЁЈ¬ЛщТФДжГьМвОӘјЩГьМвЈ¬ДжГьМвУл·сГьМвН¬ХжН¬јЩЈ¬№К¶юХЯН¬ОӘјЩГьМв;
№ШПөІ»И·¶ЁЈ¬ЛщТФДжГьМвОӘјЩГьМвЈ¬ДжГьМвУл·сГьМвН¬ХжН¬јЩЈ¬№К¶юХЯН¬ОӘјЩГьМв;
ўЮөұ![]() КұЈ¬
КұЈ¬ ![]() өД№мјЈКЗПЯ¶ОЈ¬ПФИ»ГьМвКЗјЩГьМвЈ»
өД№мјЈКЗПЯ¶ОЈ¬ПФИ»ГьМвКЗјЩГьМвЈ»
ЛщТФХжГьМвёцКэОӘ5ёц
№КСЎЈәA



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝёщҫЭЎ¶ЦР»ӘИЛГс№ІәН№ъөАВ·Ҫ»НЁ°ІИ«·ЁЎ·№ж¶ЁЈәЎ°іөБҫјЭК»ФұСӘТәҫЖҫ«ИЬ¶ИЈЁөҘО»mg/100mlЈ©/ФЪ![]() Ј¬КфУЪҫЖәујЭК»Ј»СӘТәЕЁ¶ИІ»өНУЪ80Ј¬КфУЪЧнҫЖјЭК»ЎЈЎұ2017ДкЎ°ЦРЗпҪЪЎұНн9өгҝӘКјЈ¬јГДПКРҪ»ҫҜ¶УФЪёЛКҜЗЕҪ»НЁёЪЗ°ЙиөгЈ¬¶Ф№эНщөДіөБҫҪшРРјмІйЈ¬ҫӯ№э4ёцРЎКұЈ¬№ІІйҙҰәИ№эҫЖөДјЭК»ХЯ60ГыЈ¬ПВНјКЗУГҫЖҫ«ІвКФТЗ¶ФХв60ГыјЭК»ХЯСӘТәЦРҫЖҫ«ИЬ¶ИҪшРРјмІвәуЛщөГҪб№ы»ӯіцөДЖөВК·ЦІјЦұ·ҪНјЎЈ
Ј¬КфУЪҫЖәујЭК»Ј»СӘТәЕЁ¶ИІ»өНУЪ80Ј¬КфУЪЧнҫЖјЭК»ЎЈЎұ2017ДкЎ°ЦРЗпҪЪЎұНн9өгҝӘКјЈ¬јГДПКРҪ»ҫҜ¶УФЪёЛКҜЗЕҪ»НЁёЪЗ°ЙиөгЈ¬¶Ф№эНщөДіөБҫҪшРРјмІйЈ¬ҫӯ№э4ёцРЎКұЈ¬№ІІйҙҰәИ№эҫЖөДјЭК»ХЯ60ГыЈ¬ПВНјКЗУГҫЖҫ«ІвКФТЗ¶ФХв60ГыјЭК»ХЯСӘТәЦРҫЖҫ«ИЬ¶ИҪшРРјмІвәуЛщөГҪб№ы»ӯіцөДЖөВК·ЦІјЦұ·ҪНјЎЈ
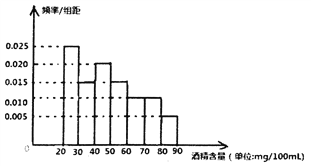
ЈЁ1Ј©ЗуХв60ГыјЭК»ХЯЦРКфУЪЧнҫЖјЭіөөДИЛКэЈЁНјЦРГҝЧй°ьАЁЧу¶ЛөгЈ¬І»°ьАЁУТ¶ЛөгЈ©
ЈЁ2Ј©ИфТФёчРЎЧйөДЦРЦөОӘёГЧйөД№АјЖЦөЈ¬ЖөВКОӘёЕВКөД№АјЖЦөЈ¬ЗуХв60ГыјЭК»ХЯСӘТәөДҫЖҫ«ЕЁ¶ИөДЖҪҫщЦөЎЈ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЦұҪЗЧшұкПө![]() ЦРЈ¬ТФ
ЦРЈ¬ТФ![]() ОӘј«өгЈ¬
ОӘј«өгЈ¬ ![]() ЦбХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯ
ЦбХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯ![]() өДј«Чшұк·ҪіМОӘ
өДј«Чшұк·ҪіМОӘ![]() Ј¬
Ј¬ ![]() КЗЗъПЯ
КЗЗъПЯ![]() УлЦұПЯ
УлЦұПЯ![]() Јә
Јә ![]() ЈЁ
ЈЁ![]() Ј©өДҪ»өгЈЁТмУЪФӯөг
Ј©өДҪ»өгЈЁТмУЪФӯөг![]() Ј©Ј®
Ј©Ј®
ЈЁ1Ј©Рҙіц![]() Ј¬
Ј¬ ![]() өДЦұҪЗЧшұк·ҪіМЈ»
өДЦұҪЗЧшұк·ҪіМЈ»
ЈЁ2Ј©Зу№эөг![]() әНЦұПЯ
әНЦұПЯ![]() ҙ№ЦұөДЦұПЯ
ҙ№ЦұөДЦұПЯ![]() өДј«Чшұк·ҪіМЈ®
өДј«Чшұк·ҪіМЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘПтБҝaЈҪ(2xЈӯyЈ«1Ј¬xЈ«yЈӯ2)Ј¬bЈҪ(2Ј¬Јӯ2).
ўЩөұxЎўyОӘәОЦөКұЈ¬aУлb№ІПЯЈҝ
ўЪКЗ·сҙжФЪКөКэxЎўyЈ¬К№өГaЎНbЈ¬ЗТ|a|ЈҪ|b|ЈҝИфҙжФЪЈ¬ЗуіцxyөДЦөЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЛДАвЧ¶![]() ЦРЈ¬ЖҪГж
ЦРЈ¬ЖҪГж![]() ЖҪГж
ЖҪГж![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() .
.
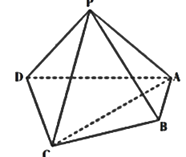
ЈЁ1Ј©ЗуЦӨЈә ![]() ЖҪГж
ЖҪГж![]() Ј»
Ј»
ЈЁ2Ј©ЗуЛДГжМе![]() өДМе»э.
өДМе»э.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() .
.
ЈЁ1Ј©Иф![]() Ј¬әҜКэ
Ј¬әҜКэ![]() өДНјПсУләҜКэ
өДНјПсУләҜКэ![]() өДНјПсПаЗРЈ¬Зу
өДНјПсПаЗРЈ¬Зу![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©Иф![]() Ј¬
Ј¬ ![]() Ј¬әҜКэ
Ј¬әҜКэ![]() ВъЧг¶ФИОТв
ВъЧг¶ФИОТв![]() Ј¬¶јУР
Ј¬¶јУР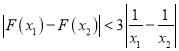 әгіЙБўЈ¬Зу
әгіЙБўЈ¬Зу![]() өДИЎЦө·¶О§Ј»
өДИЎЦө·¶О§Ј»
ЈЁ3Ј©Иф![]() Ј¬әҜКэ
Ј¬әҜКэ![]() ,ЗТ
,ЗТ![]() УРБҪёцј«Цөөг
УРБҪёцј«Цөөг![]() Ј¬ЖдЦР
Ј¬ЖдЦР![]() Ј¬Зу
Ј¬Зу![]() өДЧоРЎЦө.
өДЧоРЎЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэf(x)= ![]() Јӯ
Јӯ![]() Ј¬g(x)=
Ј¬g(x)= ![]() Ј®
Ј®
ЈЁ1Ј©Иф![]() Ј¬әҜКэ
Ј¬әҜКэ![]() өДНјПсУләҜКэ
өДНјПсУләҜКэ![]() өДНјПсПаЗРЈ¬Зу
өДНјПсПаЗРЈ¬Зу![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©Иф![]() Ј¬
Ј¬ ![]() Ј¬әҜКэ
Ј¬әҜКэ![]() ВъЧг¶ФИОТв
ВъЧг¶ФИОТв![]() ЈЁx1
ЈЁx1![]() x2Ј©Ј¬¶јУР
x2Ј©Ј¬¶јУР![]() әгіЙБўЈ¬Зу
әгіЙБўЈ¬Зу![]() өДИЎЦө·¶О§Ј»
өДИЎЦө·¶О§Ј»
ЈЁ3Ј©Иф![]() Ј¬әҜКэ
Ј¬әҜКэ![]() =f(x)+ g(x),ЗТG(
=f(x)+ g(x),ЗТG(![]() )УРБҪёцј«Цөөгx1,x2,ЖдЦРx1
)УРБҪёцј«Цөөгx1,x2,ЖдЦРx1![]() Ј¬Зу
Ј¬Зу![]() өДЧоРЎЦөЈ®
өДЧоРЎЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() .
.
ЈЁ1Ј©өұ![]() КұЈ¬ЗуәҜКэ
КұЈ¬ЗуәҜКэ![]() өДНјПуФЪ
өДНјПуФЪ![]() ҙҰөДЗРПЯ·ҪіМЈ»
ҙҰөДЗРПЯ·ҪіМЈ»
ЈЁ2Ј©ИфәҜКэ![]() ФЪ¶ЁТеУтЙПОӘөҘөчФцәҜКэ.
ФЪ¶ЁТеУтЙПОӘөҘөчФцәҜКэ.
ўЩЗу![]() ЧоҙуХыКэЦөЈ»
ЧоҙуХыКэЦөЈ»
ўЪЦӨГчЈә ![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝјЧЎўТТБҪИЛҪшРРЙд»чұИИьЈ¬ёчЙд»ч![]() ҫЦЈ¬ГҝҫЦЙд»ч
ҫЦЈ¬ГҝҫЦЙд»ч![]() ҙОЈ¬Йд»чГьЦРДҝұкөГ
ҙОЈ¬Йд»чГьЦРДҝұкөГ![]() ·ЦЈ¬ОҙГьЦРДҝұкөГ
·ЦЈ¬ОҙГьЦРДҝұкөГ![]() ·ЦЈ¬БҪИЛ
·ЦЈ¬БҪИЛ![]() ҫЦөДөГ·ЦЗйҝцИзПВЈә
ҫЦөДөГ·ЦЗйҝцИзПВЈә
јЧ |
|
|
|
|
ТТ |
|
|
|
|
ЈЁўсЈ©ИфҙУјЧөД![]() ҫЦұИИьЦРЈ¬Лж»ъСЎИЎ
ҫЦұИИьЦРЈ¬Лж»ъСЎИЎ![]() ҫЦЈ¬ЗуХв
ҫЦЈ¬ЗуХв![]() ҫЦөДөГ·ЦЗЎәГПаөИөДёЕВКЈ®
ҫЦөДөГ·ЦЗЎәГПаөИөДёЕВКЈ®
ЈЁўтЈ©Из№ы![]() Ј¬ҙУјЧЎўТТБҪИЛөД
Ј¬ҙУјЧЎўТТБҪИЛөД![]() ҫЦұИИьЦРЛж»ъёчСЎИЎ
ҫЦұИИьЦРЛж»ъёчСЎИЎ![]() ҫЦЈ¬јЗХв
ҫЦЈ¬јЗХв![]() ҫЦөДөГ·ЦәНОӘ
ҫЦөДөГ·ЦәНОӘ![]() Ј¬Зу
Ј¬Зу![]() өД·ЦІјБРәНКэС§ЖЪНыЈ®
өД·ЦІјБРәНКэС§ЖЪНыЈ®
ЈЁўуЈ©ФЪ![]() ҫЦұИИьЦРЈ¬ИфјЧЎўТТБҪИЛөДЖҪҫщөГ·ЦПаН¬Ј¬ЗТТТөД·ў»УёьОИ¶ЁЈ¬Рҙіц
ҫЦұИИьЦРЈ¬ИфјЧЎўТТБҪИЛөДЖҪҫщөГ·ЦПаН¬Ј¬ЗТТТөД·ў»УёьОИ¶ЁЈ¬Рҙіц![]() өДЛщУРҝЙДЬИЎЦөЈ®ЈЁҪбВЫІ»ТӘЗуЦӨГчЈ©
өДЛщУРҝЙДЬИЎЦөЈ®ЈЁҪбВЫІ»ТӘЗуЦӨГчЈ©
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com