考点:两角和与差的正弦函数,数量积判断两个平面向量的垂直关系,三角函数的最值
专题:平面向量及应用
分析:(1)由题意可证(
+
)•(
-
)=0,即可得结论;
(2)由题意可得
+与
+,进而可得|
+
|
2-3和|
+
|
2-3的表达式,进而可得f(x)=-8(sinx+
)
2+
,由二次函数区间的最值可得.
解答:
解:(1)由题意可得(
+
)•(
-
)=
2-
2=(cos
2x+sin
2x)-(cos
2+sin
2)=1-1=0;
∴(
+
)⊥(
-
);
(2)由题意可得
+=(cos
x+1,sin
x-1),
+=(cos
+1,-sin
-1),
∴|
+
|
2-3=(cos
x+1)
2+(sin
x-1)
2-3=2cos
x-2sin
x,
同理可得|
+
|
2-3=2cos
+2sin
,
∴f(x)=(|
+
|
2-3)(|
+
|
2-3)
=(2cos
x-2sin
x)(2cos
+2sin
)
=4(cos
xcos
+cos
xsin
-sin
xcos
-sin
xsin
)
=4(cos2x-sinx)=-8sin
2x-4sinx+4
=-8(sinx+
)
2+
由二次函数的知识可知:
当sinx=
-时,f(x)取最大值
,
当sinx=1时,f(x)取最小值-8
点评:本题考查向量和三角函数的综合应用,涉及二次函数区间的最值,属基础题.



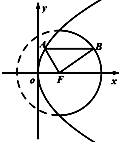 已知△ABF,点F(2,0),点A,B分别在图中抛物线y2=8x及圆(x-2)2+y2=16的实线部分上运动,且AB总是平行于x轴,则△ABF的周长的取值范围是
已知△ABF,点F(2,0),点A,B分别在图中抛物线y2=8x及圆(x-2)2+y2=16的实线部分上运动,且AB总是平行于x轴,则△ABF的周长的取值范围是