
定义在R上的单调函数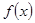 满足
满足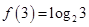 且对任意
且对任意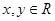 都有
都有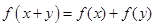 .
.
(1)求证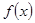 为奇函数;
为奇函数;
(2)若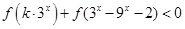 对任意
对任意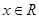 恒成立,求实数
恒成立,求实数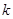 的取值范围.
的取值范围.
(1)证明:利用“赋值法”,确定f(0)=0,再
计算f(x)+f(-x)=0.
(2) t=3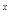 >0,换元后,问题等价于t
>0,换元后,问题等价于t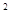 -(1+k)t+2>0
-(1+k)t+2>0
假设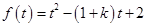 ,当
,当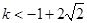 时,
时, 对任意
对任意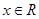 恒成立.
恒成立.
【解析】
试题分析:
思路分析:(1)证明:利用“赋值法”,确定f(0)=0,再
计算f(x)+f(-x)=0.
(2) t=3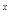 >0,换元后,问题等价于t
>0,换元后,问题等价于t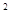 -(1+k)t+2>0
-(1+k)t+2>0
假设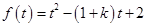 ,应用二次函数的图象和性质进一步求解。
,应用二次函数的图象和性质进一步求解。
(1)证明:f(x+y)=f(x)+f(y) (x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,
则有0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,
所以f(x)是奇函数.
(2)解: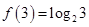 >0,即f(3)>f(0),又
>0,即f(3)>f(0),又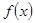 在R上是单调函数,
在R上是单调函数,
所以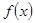 在R上是增函数
在R上是增函数
又由(1)f(x)是奇函数.f(k·3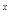 )<-f(3
)<-f(3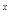 -9
-9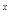 -2)=f(-3
-2)=f(-3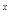 +9
+9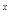 +2),
+2),
∴ k·3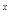 <-3
<-3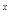 +9
+9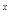 +2,3
+2,3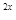 -(1+k)·3
-(1+k)·3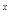 +2>0对任意x∈R成立.
+2>0对任意x∈R成立.
令t=3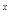 >0,问题等价于t
>0,问题等价于t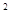 -(1+k)t+2>0
-(1+k)t+2>0
对任意t>0恒成立.
令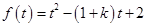 ,其对称轴
,其对称轴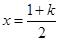
当 即
即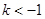 时,
时,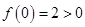 符合题意;
符合题意;
当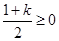 时,对任意
时,对任意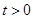 ,
, 恒成立
恒成立
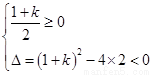
解得
综上所述,当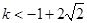 时,
时, 对任意
对任意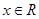 恒成立.
恒成立.
考点:函数的单调性,指数函数的性质,二次函数的图象和性质。
点评:中档题,本题涉及抽象函数问题,一般要考虑应用“赋值法”,确定所需数据。本题通过换元,将问题转化成二次函数的图象和性质应用问题,具有“化生为熟”的示范作用。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2-x | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(-2-an) |
| 1 |
| 2 |
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
| 4 |
| 3 |
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| a2n |
| 12 |
| 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
| 1 |
| 2n |
| 4 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com