
【题目】某企业拟对某条生产线进行技术升级,现有两种方案可供选择:方案![]() 是报废原有生产线,重建一条新的生产线;方案
是报废原有生产线,重建一条新的生产线;方案![]() 是对原有生产线进行技术改造.由于受诸多不可控因素的影响,市场销售状态可能会发生变化.该企业管理者对历年产品销售市场行情及回报率进行了调研,编制出下表:
是对原有生产线进行技术改造.由于受诸多不可控因素的影响,市场销售状态可能会发生变化.该企业管理者对历年产品销售市场行情及回报率进行了调研,编制出下表:
市场销售状态 | 畅销 | 平销 | 滞销 | |
市场销售状态概率 |
|
|
| |
预期平均年利润(单位:万元) | 方案 | 700 | 400 |
|
方案 | 600 | 300 |
| |
(1)以预期平均年利润的期望值为决策依据,问:该企业应选择哪种方案?
(2)记该生产线升级后的产品(以下简称“新产品”)的年产量为![]() (万件),通过核算,实行方案
(万件),通过核算,实行方案![]() 时新产品的年度总成本
时新产品的年度总成本![]() (万元)为
(万元)为![]() ,实行方案
,实行方案时新产品的年度总成本
![]() (万元)为
(万元)为![]() .已知
.已知![]() ,
,![]() .若按(1)的标准选择方案,则市场行情为畅销、平销和滞销时,新产品的单价
.若按(1)的标准选择方案,则市场行情为畅销、平销和滞销时,新产品的单价![]() (元)分别为60,
(元)分别为60,![]() ,
,![]() ,且生产的新产品当年都能卖出去.试问:当
,且生产的新产品当年都能卖出去.试问:当![]() 取何值时,新产品年利润
取何值时,新产品年利润![]() 的期望取得最大值?并判断这一年利润能否达到预期目标.
的期望取得最大值?并判断这一年利润能否达到预期目标.
【答案】(1)当![]() 时,应选择方程
时,应选择方程![]() ;当
;当![]() 时应选择方程
时应选择方程![]() ;(2)年产量为10万件的情况下,可以达到甚至超过预期的平均年利润.
;(2)年产量为10万件的情况下,可以达到甚至超过预期的平均年利润.
【解析】
(1)根据表格数据计算出两种方案的平均年利润的期望值,比较可得;
(2)求出方案![]() ,按市场销售状态的新产品的年利润
,按市场销售状态的新产品的年利润![]() 的分布列,求出期望值,再用导数的知识求得最大值即可.
的分布列,求出期望值,再用导数的知识求得最大值即可.
解:(1)∵ ,解得
,解得![]() .
.
![]() ,
,
![]() ,
,
![]() ;
;
![]() ;
;![]() .
.
∴当![]() 时,应选择方程
时,应选择方程![]() ;当
;当![]() 时应选择方程
时应选择方程![]() ;
;
当![]() 时,根据(1)的结果,应选择方案
时,根据(1)的结果,应选择方案![]() ,所以新产品的年度总成本为
,所以新产品的年度总成本为
![]() .
.
(2)设市场行情为畅销、平销和滞销时,新产品的年利润分别为![]() ,
,![]() 和
和![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
∴![]() 的分布列为
的分布列为
|
|
|
|
| 0.4 | 0.4 | 0.2 |
![]()
![]() .
.
设![]() ,
,![]() ,
,
∴![]() .
.
![]() ,
,![]() .
.
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() 取得最大值,即年产量为10万件时,
取得最大值,即年产量为10万件时,![]() 取得最大值,
取得最大值,
此时![]() (万元).
(万元).
由(1)知,预期平均年利润的期望![]() (万元).
(万元).
因为![]() ,所以在年产量为10万件的情况下,可以达到甚至超过预期的平均年利润.
,所以在年产量为10万件的情况下,可以达到甚至超过预期的平均年利润.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,点
为平行四边形,点![]() 在面
在面![]() 内的射影为
内的射影为![]() ,
,![]() ,点
,点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,且直线
,且直线![]() 与
与![]() 垂直.
垂直.
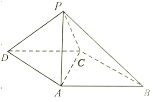
(Ⅰ)在棱![]() 上找一点
上找一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 平行,并说明理由;
平行,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,棱长为2,
中,棱长为2,![]() 分别为棱
分别为棱![]() 的中点,
的中点,![]() 为底面正方形
为底面正方形![]() 内一点(含边界)且
内一点(含边界)且![]() 与面
与面![]() 所成角的正切值为
所成角的正切值为![]() ,直线
,直线![]() 与面
与面![]() 的交点为
的交点为![]() ,当
,当![]() 到
到![]() 的距离最小时,则四面体
的距离最小时,则四面体![]() 外接球的表面积为___________.
外接球的表面积为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为![]() 和
和![]() 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为![]() ,宽为内接正方形的边长
,宽为内接正方形的边长![]() .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设![]() 为斜边
为斜边![]() 的中点,作直角三角形
的中点,作直角三角形![]() 的内接正方形对角线
的内接正方形对角线![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则下列推理正确的是( )
,则下列推理正确的是( )
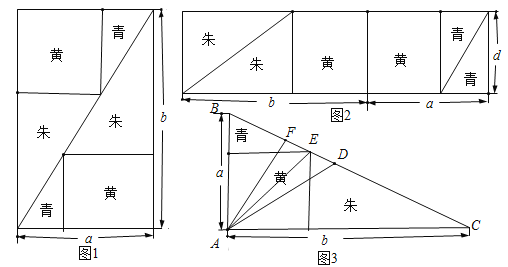
①由图1和图2面积相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得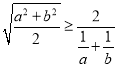 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,上顶点坐标为
,上顶点坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)问是否存在斜率为1的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点,![]() ,
,![]() 的重心分别为
的重心分别为![]() ,且以线段
,且以线段![]() 直径的圆过原点,若存在,求出直线
直径的圆过原点,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十八大以来,党中央提出要在2020年实现全面脱贫,为了实现这一目标,国家对“新农合”(新型农村合作医疗)推出了新政,各级财政提高了对“新农合”的补助标准.提高了各项报销的比例,其中门诊报销比例如下:
表1:新农合门诊报销比例
医院类别 | 村卫生室 | 镇卫生院 | 二甲医院 | 三甲医院 |
门诊报销比例 | 60% | 40% | 30% | 20% |
根据以往的数据统计,李村一个结算年度门诊就诊人次情况如下:
表2:李村一个结算年度门诊就诊情况统计表
医院类别 | 村卫生室 | 镇卫生院 | 二甲医院 | 三甲医院 |
一个结算年度内各门诊就诊人次占李村总就诊人次的比例 | 70% | 10% | 15% | 5% |
如果一个结算年度每人次到村卫生室、镇卫生院、二甲医院、三甲医院门诊平均费用分别为50元、100元、200元、500元.若李村一个结算年度内去门诊就诊人次为2000人次.
(Ⅰ)李村在这个结算年度内去三甲医院门诊就诊的人次中,60岁以上的人次占了80%,从去三甲医院门诊就诊的人次中任选2人次,恰好2人次都是60岁以上人次的概率是多少?
(Ⅱ)如果将李村这个结算年度内门诊就诊人次占全村总就诊人次的比例视为概率,求李村这个结算年度每人次用于门诊实付费用(报销后个人应承担部分)![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科学家为研究对某病毒有效的疫苗,通过小鼠进行毒性和药效预实验.已知5只小鼠中有1只患有这种病毒引起的疾病,需要通过化验血液来确定患病的小鼠.血液化验结果呈阳性的即为患病小鼠,呈阴性即没患病.下面是两种化验方案:
方案甲:逐个化验,直到能确定患病小鼠为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病小鼠为止;若结果呈阴性则在另外2只中任取1只化验.
(1)求方案甲化验次数X的分布列;
(2)判断哪一个方案的效率更高,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com