
【题目】如图,抛物线关于![]() 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点![]() 、
、![]() 、
、![]() 均在抛物线上.
均在抛物线上.
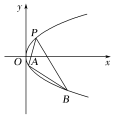
(1)写出该抛物线的方程及其准线方程;
(2)当![]() 与
与![]() 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求![]() 的值及直线
的值及直线![]() 的斜率.
的斜率.
科目:高中数学 来源: 题型:
【题目】某校针对校食堂饭菜质量开展问卷调查,提供满意与不满意两种回答,调查结果如下表(单位:人):
学生 | 高一 | 高二 | 高三 |
满意 | 500 | 600 | 800 |
不满意 | 300 | 200 | 400 |
(1)求从所有参与调查的人中任选1人是高三学生的概率;
(2)从参与调查的高三学生中,用分层抽样的方法抽取6人,在这6人中任意选取2人,求这两人对校食堂饭菜质量都满意的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}和{bn}是两个等差数列,记cn=max{b1-a1n,b2-a2n,…,bn-ann}(n=1,2,3,…),其中max{x1,x2,…,xs}表示x1,x2,…,xs这s个数中最大的数.
(Ⅰ)若an=n,bn=2n-1,求c1,c2,c3的值,并证明{cn}是等差数列;
(Ⅱ)证明:或者对任意正数M,存在正整数m,当n≥m时, ![]() >M;或者存在正整数m,使得cm,cm+1,cm+2,…是等差数列.
>M;或者存在正整数m,使得cm,cm+1,cm+2,…是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对定义域内的每一个值
对定义域内的每一个值![]() ,在其定义域内都存在唯一的
,在其定义域内都存在唯一的![]() ,使
,使![]() 成立,则该函数为“依附函数”.
成立,则该函数为“依附函数”.
(1)判断函数![]() 是否为“依附函数”,并说明理由;
是否为“依附函数”,并说明理由;
(2)若函数![]() 在定义域
在定义域![]() 上“依附函数”,求
上“依附函数”,求![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在定义域
在定义域![]() 上为“依附函数”.若存在实数
上为“依附函数”.若存在实数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 都成立,求实数
都成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从全校参加科技知识竞赛初赛的学生试卷中,抽取一个样本,考察竞赛的成绩分布.将样本分成5组,绘成频率分布直方图(如图),图中从左到右各小组的小长方形的高之比是![]() ,最后一组的频数是6.请结合频率分布直方图提供的信息,解答下列问题:
,最后一组的频数是6.请结合频率分布直方图提供的信息,解答下列问题:
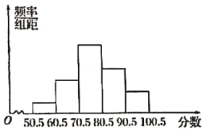
(1)样本的容量是多少?
(2)求样本中成绩在![]() 分的学生人数;
分的学生人数;
(3)从样本中成绩在90.5分以上的同学中随机地抽取2人参加决赛,求最高分甲被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某汽车品牌一个月内被消费者投诉的次数用![]() 表示,据统计,随机变量
表示,据统计,随机变量![]() 的概率分布如下:
的概率分布如下:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
(1)求![]() 的值;
的值;
(2)若每个月被消费者投诉的次数互不影响,求该汽车品牌在五个月内被消费者投诉3次的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com