
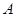 是棱长为
是棱长为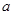 的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有
的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有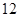 个顶点;②有
个顶点;②有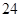 条棱;③有
条棱;③有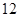 个面;④表面积为
个面;④表面积为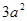 ;⑤体积为
;⑤体积为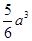 .其中正确的结论是____________.(要求填上所有正确结论的序号)
.其中正确的结论是____________.(要求填上所有正确结论的序号)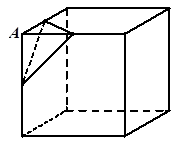
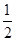 ×48=24条棱.②正确;
×48=24条棱.②正确;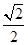 a,所以正方形总面积为6×
a,所以正方形总面积为6×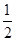 ×a2=3a2,三角形总面积为8×
×a2=3a2,三角形总面积为8×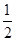 ×
×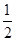 a2sin60°=
a2sin60°= a2,表面积(3+
a2,表面积(3+ )a2,故④错;
)a2,故④错; (
( )3=
)3= a2,剩余总体积为a3-
a2,剩余总体积为a3- a3=
a3=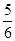 a3⑤正确.
a3⑤正确.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com