
【题目】从某高中学生的体能测试结果中,随机抽取100名学生的测试结果,按体重分组得到如图所示的频率分布直方图.
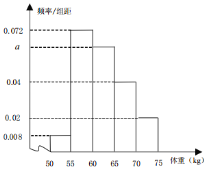
(1)若该校约有![]() 的学生体重不超过“标准体重
的学生体重不超过“标准体重![]() ”,试估计
”,试估计![]() 的值,并说明理由;
的值,并说明理由;
(2)从第3、4、5组中用分层抽样的方法抽取6名学生进行了第二次测试,现从这6人中随机抽取2人进行日常运动习惯的问卷调查,求抽到4组的人数![]() 的分布列及期望.
的分布列及期望.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的右焦点为F,左顶点为A,离心率
)的右焦点为F,左顶点为A,离心率![]() ,且经过圆O:
,且经过圆O:![]() 的圆心.过点F作不与坐标轴重合的直线
的圆心.过点F作不与坐标轴重合的直线![]() 和该椭圆交于MN两点,且直线
和该椭圆交于MN两点,且直线![]()
![]() 分别与直线
分别与直线![]() 交于PQ两点.
交于PQ两点.
(1)求椭圆的方程;
(2)证明:![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为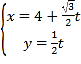 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)在曲线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,求
,求![]() 点轨迹的极坐标方程;
点轨迹的极坐标方程;
(2)在曲线![]() 上任取一点
上任取一点![]() ,在曲线
,在曲线![]() 上任取一点
上任取一点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由郭帆执导吴京主演的电影《流浪地球》于2019年2月5日起在中国内地上映,影片引发了观影热潮,预计《流浪地球》票房收入47亿人民币,超过《红海行动》成为中国影史票房亚军,仅次于《战狼2》.某电影院为了解该影院观看《流浪地球》的观众的年龄构成情况,随机抽取了40名观众,将他们的年龄分成7段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
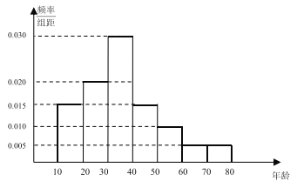
(1)试求这40名观众年龄的平均数、中位数、众数;
(2)(i)若从样本中年龄在50岁以上的观众中任取3名赠送VIP贵宾观影卡,求这3名观众至少有1人年龄不低于70岁的概率;
(ii)该电影院决定采用抽奖方式来提升观影人数,将《流浪地球》电影票票价提高20元,并允许购买电影票的观众抽奖3次,中奖1次、2次、3次分别奖现金![]() 元、
元、![]() 元,
元,![]() 元.设观众每次中奖的概率均为
元.设观众每次中奖的概率均为![]() ,若要使抽奖方案对电影院有利,则
,若要使抽奖方案对电影院有利,则![]() 最高可定为多少元?(结果精确到个位)
最高可定为多少元?(结果精确到个位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率等于
)的离心率等于![]() ,它的一个长轴端点恰好是抛物线
,它的一个长轴端点恰好是抛物线![]() 的焦点.
的焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,且直线
有且只有一个公共点,且直线![]() 与直线
与直线![]() 和
和![]() 分别交于
分别交于![]() 两点,试探究以线段
两点,试探究以线段![]() 为直径的圆是否恒过定点?若恒过定点,求出该定点,若不恒过定点,请说明理由.
为直径的圆是否恒过定点?若恒过定点,求出该定点,若不恒过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(ωx+φ)![]() cos(ωx+φ)(ω>0,|φ|
cos(ωx+φ)(ω>0,|φ|![]() )的图象与直线y=2的两个相邻的交点之间的距离为π,且f(x)+f(﹣x)=0,若g(x)=sin(ωx+φ),则( )
)的图象与直线y=2的两个相邻的交点之间的距离为π,且f(x)+f(﹣x)=0,若g(x)=sin(ωx+φ),则( )
A.g(x)在(0,![]() )上单调递增B.g(x)在 (0,
)上单调递增B.g(x)在 (0,![]() )上单调递减
)上单调递减
C.g(x)在(![]() ,
,![]() )上单调递增D.g(x)在(
)上单调递增D.g(x)在(![]() ,
,![]() )上单调递减
)上单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:区间![]() ,
,![]() ,
,![]() ,
,![]() 的长度均为
的长度均为![]() ,若不等式
,若不等式![]() 的解集是互不相交区间的并集,设该不等式的解集中所有区间的长度之和为
的解集是互不相交区间的并集,设该不等式的解集中所有区间的长度之和为![]() ,则( )
,则( )
A. 当![]() 时,
时,![]() B. 当
B. 当![]() 时,
时,![]()
C. 当![]() 时,
时,![]() D. 当
D. 当![]() 时,
时,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推行“高中新课程改革”,某数学老师分别用“传统教学”和“新课程”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果.期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于120分者为“成绩优良”.
分数 |
|
|
|
|
|
甲班频数 | 7 | 5 | 4 | 3 | 1 |
乙班频数 | 1 | 2 | 5 | 5 | 7 |
(1)从以上统计数据填写下面![]() 列联表,并判断能否犯错误的频率不超过0.01的前提下认为“成绩优良与教学方式有关”?
列联表,并判断能否犯错误的频率不超过0.01的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
P( | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
附: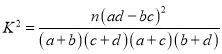 ,其中
,其中![]() .临界值表如上表:
.临界值表如上表:
(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核,在这8人中,记成绩不优良的乙班人数为X,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com