
【题目】已知函数![]() 有三个不同的零点
有三个不同的零点![]() ,
, ![]() ,
, ![]() (其中
(其中![]() ),则
),则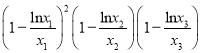 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】令f(x)=0,分离变量可得a=![]() ,
,
令g(x)=![]() ,
,
由g′(x)= =0,得x=1或x=e.
=0,得x=1或x=e.
当x∈(0,1)时,g′(x)<0;当x∈(1,e)时,g′(x)>0;当x∈(e,+∞)时,g′(x)<0.
即g(x)在(0,1),(e,+∞)上为减函数,在(1,e)上为增函数.
∴0<x1<1<x2<e<x3,
a=![]() =
= ,令μ=
,令μ=![]() ,
,
则a=![]() ﹣μ,即μ2+(a﹣1)μ+1﹣a=0,
﹣μ,即μ2+(a﹣1)μ+1﹣a=0,
μ1+μ2=1﹣a<0,μ1μ2=1﹣a<0,
对于μ=![]() ,μ′=
,μ′=![]()
则当0<x<e时,μ′>0;当x>e时,μ′<0.而当x>e时,μ恒大于0.
画其简图,

不妨设μ1<μ2,则μ1=![]() ,μ2=
,μ2=![]() =
=![]() =μ3,
=μ3,
∴(1﹣![]() )2(1﹣
)2(1﹣![]() )(1﹣
)(1﹣![]() )=(1﹣μ1)2(1﹣μ2)(1﹣μ3)
)=(1﹣μ1)2(1﹣μ2)(1﹣μ3)
=[(1﹣μ1)(1﹣μ2)]2=[1﹣(1﹣a)+(1﹣a)]2=1.
故选:D.


科目:高中数学 来源: 题型:
【题目】如图,A是△BCD所在平面外一点,M、N为△ABC和△ACD重心,BD=6; 
(1)求MN的长;
(2)若A、C的位置发生变化,MN的位置和长度会改变吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某餐厅装修,需要大块胶合板![]() 张,小块胶合板
张,小块胶合板![]() 张,已知市场出售
张,已知市场出售![]() 两种不同规格的胶合板。经过测算,
两种不同规格的胶合板。经过测算, ![]() 种规格的胶合板可同时截得大块胶合板
种规格的胶合板可同时截得大块胶合板![]() 张,小块胶合板
张,小块胶合板![]() 张,
张, ![]() 种规格的胶合板可同时截得大块胶合板
种规格的胶合板可同时截得大块胶合板![]() 张,小块胶合板
张,小块胶合板![]() 张.已知
张.已知![]() 种规格胶合板每张
种规格胶合板每张![]() 元,
元, ![]() 种规格胶合板每张
种规格胶合板每张![]() 元.分别用
元.分别用![]() 表示购买
表示购买![]() 两种不同规格的胶合板的张数.
两种不同规格的胶合板的张数.
(1)用![]() 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;
(2)根据施工需求, ![]() 两种不同规格的胶合板各买多少张花费资金最少?并求出最少资金数.
两种不同规格的胶合板各买多少张花费资金最少?并求出最少资金数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一张纸沿直线l对折一次后,点A(0,4)与点B(8,0)重叠,点C(6,8)与点D(m,n)重叠.
(1)求直线l的方程;
(2)求m+n的值;
(3)直线l上是否存在一点P,使得||PB|﹣|PC||存在最大值,如果存在,请求出最大值,以及此时点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=2sin(2x+ ![]() )的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的
)的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的 ![]() 倍,所得图象关于直线x=
倍,所得图象关于直线x= ![]() 对称,则φ的最小正值为 .
对称,则φ的最小正值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,若存在非零实数m,使得对于任意x∈M(MD),有(x﹣m)∈D且f(x﹣m)≤f(x),则称f(x)为M上的m度低调函数.如果定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x﹣a2|﹣a2 , 且f(x)为R上的5度低调函数,那么实数a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的序号是 . ①y=﹣2cos( ![]() π﹣2x)是奇函数;
π﹣2x)是奇函数;
②若α,β是第一象限角,且α>β,则sinα>sinβ;
③x=﹣ ![]() 是函数y=3sin(2x﹣
是函数y=3sin(2x﹣ ![]() )的一条对称轴;
)的一条对称轴;
④函数y=sin( ![]() ﹣2x)的单调减区间是[kπ﹣
﹣2x)的单调减区间是[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为C的圆过点A(0,﹣6)和B(1,﹣5),且圆心在直线l:x﹣y+1=0上.
(1)求圆心为C的圆的标准方程;
(2)过点M(2,8)作圆的切线,求切线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com