
【题目】已知正整数![]() ,设长方形
,设长方形![]() 的边长
的边长![]() ,
,![]() ,边
,边![]() 、
、![]() 、
、![]() 上的点
上的点![]() ,
,![]() …,
…,![]() ,
,![]() ,
,![]() …,
…,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分别满足
分别满足![]() ,
,![]() ,
, ![]() .
.
(1)对于![]() ,2,…,
,2,…,![]() ,求
,求![]() 与
与![]() 、
、![]() 与
与![]() 的交点所在的二次曲线
的交点所在的二次曲线![]() 的方程;
的方程;
(2)若![]() 的延长线上的点
的延长线上的点![]() ,
,![]() ,…,
,…,![]() 满足
满足![]() ,对于
,对于![]() ,2,…,
,2,…,![]() ,求
,求![]() 与
与![]() 的交点所在的二次曲线
的交点所在的二次曲线![]() 的方程;
的方程;
(3)设在二次曲线![]() 上到
上到![]() 的距离最大的点为
的距离最大的点为![]() ,求
,求![]() 与二次曲线
与二次曲线![]() 上的点的距离的最小值.
上的点的距离的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】2019年元旦班级联欢晚会上,某班在联欢会上设计了一个摸球表演节目的游戏,在一个纸盒中装有1个红球,1个黄球,1个白球和1个黑球,这些球除颜色外完全相同,A同学不放回地每次摸出1个球,若摸到黑球则停止摸球,否则就要将纸盒中的球全部摸出才停止.规定摸到红球表演两个节目,摸到白球或黄球表演一个节目,摸到黑球不用表演节目.
(1)求A同学摸球三次后停止摸球的概率;
(2)记X为A同学摸球后表演节目的个数,求随机变量X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数. 设
为自然对数的底数. 设![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)若![]() 时,函数
时,函数![]() 在
在![]() 处的切线经过点
处的切线经过点![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的单调区间;
上的单调区间;
(Ⅲ)若![]() ,函数
,函数![]() 在区间
在区间![]() 内有零点,求
内有零点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
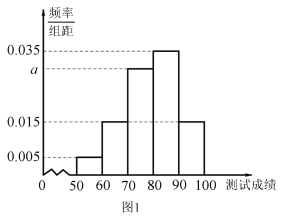
【题目】顺义区教委对本区高一,高二年级学生体质健康测试成绩进行抽样分析.学生测试成绩满分为100分,90分及以上为优秀,60分以下为不及格.先从两个年级各抽取100名学生的测试成绩.其中高一年级学生测试成绩统计结果如图1,高二年级学生测试成绩统计结果如表1.
分组 | 人数 |
|
|
|
|
|
|
|
|
|
|
表1
(1)求图1中a的值;
(2)为了调查测试成绩不及格的同学的具体情况,决定从样本中不及格的学生中抽取3人,用X表示抽取的3人中高二年级的学生人数.求X的分布列及均值;
(3)若用以上抽样数据估计全区学生体质健康情况.用Y表示从全区高二年级全部学生中任取3人中成绩优秀的人数,求EY的值;
(4)用![]() ,
,![]() ,分别表示样本中高一,高二年级学生测试成绩的方差,比较其大小(只需写出结果).
,分别表示样本中高一,高二年级学生测试成绩的方差,比较其大小(只需写出结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王明、李东、张红三位同学在第一、第二学期消费的部分文具的数量如表所示:
姓名 | 第一学期 | 第二学期 | ||||||
笔记本 | 练习本 | 水笔 | 铅笔 | 笔记本 | 练习本 | 水笔 | 铅笔 | |
王明 | 3 | 5 | 2 | 4 | 4 | 6 | 3 | 3 |
李东 | 2 | 6 | 3 | 3 | 4 | 8 | 5 | 2 |
张红 | 4 | 7 | 4 | 2 | 5 | 10 | 6 | 4 |
若笔记本的单价为每本5元;练习本每本2元;水笔每支3元;铅笔每支1元.求三位学生在这些文具上各自花费的金额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查。现在按课外阅读时间的情况将学生分成三类:A类(不参加课外阅读),B类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),C类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时)。调查结果如下表:
A类 | B类 | C类 | |
男生 | x | 5 | 3 |
女生 | y | 3 | 3 |
(I)求出表中x,y的值;
(II)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | |
不参加课外阅读 | |||
参加课外阅读 | |||
总计 |
(III)从抽出的女生中再随机抽取3人进一步了解情况,记X为抽取的这3名女生中A类人数和C类人数差的绝对值,求X的数学期望。
附:K2=![]() )
)
P(K2≥k0) | 0.10 | 0.01 | |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com