
【题目】设f(x)= ![]() ,曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直. (Ⅰ)求a的值;
,曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直. (Ⅰ)求a的值;
(Ⅱ)若对于任意的x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求m的取值范围;
(Ⅲ)求证:ln(4n+1)≤16 ![]() (n∈N*).
(n∈N*).
【答案】解:(Ⅰ) 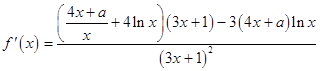 由题设f'(1)=1,∴
由题设f'(1)=1,∴ ![]() ,即a=0;
,即a=0;
(Ⅱ)解: ![]() ,x∈[1,+∞),f(x)≤m(x﹣1),即
,x∈[1,+∞),f(x)≤m(x﹣1),即 ![]() ,
,
设 ![]() ,即x∈[1,+∞),g(x)≤0.
,即x∈[1,+∞),g(x)≤0.![]() ,g'(1)=4﹣4m.
,g'(1)=4﹣4m.
② 若m≤0,g'(x)>0,g(x)≥g(1)=0,这与题设g(x)≤0矛盾;
②若m∈(0,1),当 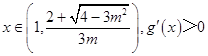 ,g(x)单调递增,g(x)>g(1)=0,与题设矛盾;
,g(x)单调递增,g(x)>g(1)=0,与题设矛盾;
③若m≥1,当x∈(1,+∞),g'(x)≤0,g(x)单调递减,g(x)≤g(1)=0,即不等式成立;
综上所述,m≥1.
(Ⅲ)证明:由(Ⅱ)知,当x>1时,m=1时, ![]() 成立.
成立.
不妨令 ![]() ,
,
∴ ![]() ,
,
即 ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() .
.
累加可得:ln(4n+1)≤16 ![]() (n∈N*)
(n∈N*)
【解析】(Ⅰ)求出原函数的导函数,结合f'(1)=1列式求得a值;(Ⅱ)把(Ⅰ)中求得的a值代入函数解析式,由f(x)≤m(x﹣1)得到 ![]() ,构造函数
,构造函数 ![]() ,即x∈[1,+∞),g(x)≤0.然后对m分类讨论求导求得m的取值范围;(Ⅲ)由(Ⅱ)知,当x>1时,m=1时,
,即x∈[1,+∞),g(x)≤0.然后对m分类讨论求导求得m的取值范围;(Ⅲ)由(Ⅱ)知,当x>1时,m=1时, ![]() 成立.令
成立.令 ![]() ,然后分别取i=1,2,…,n,利用累加法即可证明结论.
,然后分别取i=1,2,…,n,利用累加法即可证明结论.
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}的首项a1为a(a∈R).设数列的前n项和为Sn,且![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求数列{an}的通项公式及Sn;
(2)记![]() ,
,![]() .当n≥2时,求An与Bn.
.当n≥2时,求An与Bn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面内,定点A,B,C,D满足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,|
|,| ![]() ||
|| ![]() |=|
|=| ![]() ||
|| ![]() |=|
|=| ![]() ||
|| ![]() |=﹣4,动点P,M满足|
|=﹣4,动点P,M满足| ![]() |=2,
|=2, ![]() =
= ![]() ,则|
,则| ![]() |的最大值是 .
|的最大值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x2﹣1|+x2+kx,且定义域为(0,2).
(1)求关于x的方程f(x)=kx+3在(0,2)上的解;
(2)若关于x的方程f(x)=0在(0,2)上有两个的解x1 , x2 , 求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①设![]() 为直线,
为直线,![]() 为平面,且
为平面,且![]() ,则“
,则“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②若![]() 是
是![]() 的充分不必要条件,则
的充分不必要条件,则![]() 是
是![]() 的必要不充分条件;;
的必要不充分条件;;
③已知![]() ,
,![]() 为两个命题,若“
为两个命题,若“![]() ”为假命题,则“
”为假命题,则“![]() 为真命题”
为真命题”
④若不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是
的取值范围是![]() ;
;
⑤若命题![]() 有
有![]() ,则
,则![]() 有
有![]() ;
;
其中真命题的序号是____________(写出全部真命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com