
【题目】已知圆C经过P(4,-2),Q(-1,3)两点,且在y轴上截得的线段长为4![]() ,半径小于5.
,半径小于5.
(Ⅰ)求直线PQ与圆C的方程;
(Ⅱ)若直线l∥PQ,直线l与圆C交于点A,B且以线段AB为直径的圆经过坐标原点,求直线l的方程.
【答案】(1)x+y-2=0,(x-1)2+y2=13;(2)x+y-4=0或x+y+3=0。
【解析】
试题分析:(Ⅰ)直线PQ的方程为:x+y-2=0,
设圆心C(a,b)半径为r,
由于线段PQ的垂直平分线的方程是y-![]() =x-
=x-![]() ,即y=x-1,
,即y=x-1,
所以b=a-1. ①
又由在y轴上截得的线段长为4![]() ,知r2=12+a2,
,知r2=12+a2,
可得(a+1)2+(b-3)2=12+a2, ②
由①②得: a=1,b=0或a=5,b=4.
当a=1,b=0时,r2=13满足题意,
当a=5,b=4时,r2=37不满足题意,
故圆C的方程为(x-1)2+y2=13.
(Ⅱ)设直线l的方程为y=-x+m,A(x1,m-x1),B(x2,m-x2),
由题意可知OA⊥OB,即![]() =0,
=0,
∴x1x2+(m-x1)(m-x2)=0, 化简得2x1x2-m(x1+x2)+m2=0. ③
由![]() 得2x2-2(m+1)x+m2-12=0,
得2x2-2(m+1)x+m2-12=0,
∴x1+x2=m+1,x1x2=![]() .
.
代入③式,得m2-m·(1+m)+m2-12=0,
∴m=4或m=-3,经检验都满足判别式Δ>0,
∴y=-x+4或y=-x-3.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() 底面
底面![]() ,
, ![]() 为直线
为直线![]() 上一动点.
上一动点.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() ,
, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅲ)直线![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a和b是计算机在区间(0,2)上产生的均匀随机数,则一元二次不等式ax2+4x+4b>0(a>0)的解集不是R的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 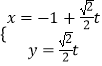 (t为参数),曲线C的极坐标方程是ρ=
(t为参数),曲线C的极坐标方程是ρ= ![]() ,以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A、B两点.
,以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A、B两点.
(Ⅰ)写出直线l的极坐标方程与曲线C的普通方程;
(Ⅱ)求线段MA、MB长度之积MAMB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆中心在坐标原点O,焦点在![]() 轴上,长轴长是短轴长的2倍,且经过点M(2,1),直线
轴上,长轴长是短轴长的2倍,且经过点M(2,1),直线![]() 平行OM,且与椭圆交于A、B两个不同的点。
平行OM,且与椭圆交于A、B两个不同的点。
(Ⅰ)求椭圆方程;
(Ⅱ)若![]() AOB为钝角,求直线
AOB为钝角,求直线![]() 在
在![]() 轴上的截距
轴上的截距![]() 的取值范围;
的取值范围;
(Ⅲ)求证直线MA、MB与![]() 轴围成的三角形总是等腰三角形。
轴围成的三角形总是等腰三角形。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos2ωx+ ![]() sin2ωx(ω>0)的最小正周期为π,给出下列四个命题:
sin2ωx(ω>0)的最小正周期为π,给出下列四个命题:
①f(x)的最大值为3;
②将f(x)的图象向左平移 ![]() 后所得的函数是偶函数;
后所得的函数是偶函数;
③f(x)在区间[﹣ ![]() ,
, ![]() ]上单调递增;
]上单调递增;
④f(x)的图象关于直线x= ![]() 对称.
对称.
其中正确说法的序号是( )
A.②③
B.①④
C.①②④
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对顾客实行购物优惠活动,规定一次购物付款总额:
(1)如果不超过200元,则不给予优惠;
(2)如果超过200元但不超过500元,则按标价给予9折优惠;
(3)如果超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予7折优惠.
某人单独购买A,B商品分别付款168元和423元,假设他一次性购买A,B两件商品,则应付款是
A. 413.7元 B. 513.7元 C. 546.6元 D. 548.7元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com