
【题目】如图,一个湖的边界是圆心为![]() 的圆,湖的一侧有一条直线型公路
的圆,湖的一侧有一条直线型公路![]() ,湖上有桥
,湖上有桥![]() (
(![]() 是圆
是圆![]() 的直径).规划在公路
的直径).规划在公路![]() 上选两个点
上选两个点![]() ,并修建两段直线型道路
,并修建两段直线型道路![]() .规划要求:线段
.规划要求:线段![]() 上的所有点到点
上的所有点到点![]() 的距离均不小于圆
的距离均不小于圆![]() 的半径.已知点
的半径.已知点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() 和
和![]() (
(![]() 为垂足),测得
为垂足),测得![]() ,
,![]() ,
,![]() (单位:百米).
(单位:百米).
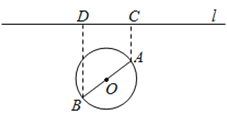
(1)若道路![]() 与桥
与桥![]() 垂直,求道路
垂直,求道路![]() 的长;
的长;
(2)在规划要求下,![]() 和
和![]() 中能否有一个点选在
中能否有一个点选在![]() 处?并说明理由.
处?并说明理由.
【答案】(1)15(百米);(2)不能,理由见解析
【解析】
(1)作![]() ,可求得
,可求得![]() ,从而得到
,从而得到![]() ,由
,由![]() 可求得结果;
可求得结果;
(2)①若![]() 在
在![]() 处,线段
处,线段![]() 上的点(除
上的点(除![]() )到点
)到点![]() 的距离均小于圆
的距离均小于圆![]() 的半径,不符合规划要求;②若
的半径,不符合规划要求;②若![]() 在
在![]() 处,可得到
处,可得到![]() ;利用余弦定理可验证出
;利用余弦定理可验证出![]() 为锐角,可知
为锐角,可知![]() 上存在点到点
上存在点到点![]() 的距离小于圆
的距离小于圆![]() 的半径,不符合规划要求;由此可得结论.
的半径,不符合规划要求;由此可得结论.
(1)过点![]() 作
作![]() ,垂足为
,垂足为![]()
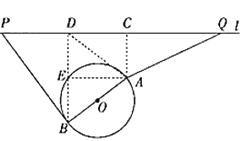
由已知条件得:四边形![]() 为矩形
为矩形 ![]() ,
,![]()
![]()
![]()

![]() 道路
道路![]() 的长为
的长为![]() (百米)
(百米)
(2)不能,理由如下:
①若![]() 在
在![]() 处,由(1)可得
处,由(1)可得![]() 在圆上
在圆上
则线段![]() 上的点(除
上的点(除![]() )到点
)到点![]() 的距离均小于圆
的距离均小于圆![]() 的半径
的半径
![]() 选在
选在![]() 处不满足规划要求
处不满足规划要求
②若![]() 在
在![]() 处,连接
处,连接![]()
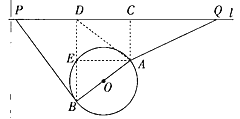
由(1)知:![]()
![]()
![]() 为锐角
为锐角 ![]() 线段
线段![]() 上存在点到点
上存在点到点![]() 的距离小于圆
的距离小于圆![]() 的半径
的半径
![]() 选在
选在![]() 处也不满足规划要求
处也不满足规划要求
综上所述:![]() 和
和![]() 均不能选在
均不能选在![]() 处
处


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
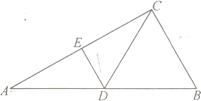
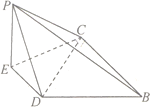
如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.经过任意三点有且只有一个平面.
B.过点![]() 有且仅有一条直线与异面直线
有且仅有一条直线与异面直线![]() 垂直.
垂直.
C.一条直线与一个平面平行,它就和这个平面内的任意一条直线平行.
D.面![]() 与平面
与平面![]() 相交,则公共点个数为有限个.
相交,则公共点个数为有限个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径![]() ,
,![]() 两点间的距离,现在珊瑚群岛上取两点
两点间的距离,现在珊瑚群岛上取两点![]() ,
,![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() 两点的距离为___.
两点的距离为___.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是海面上一条南北方向的海防警戒线,在
是海面上一条南北方向的海防警戒线,在 ![]() 上点
上点 ![]() 处有一个水声监测点,另两个监测点
处有一个水声监测点,另两个监测点 ![]() 分别在
分别在 ![]() 的正东方向
的正东方向 ![]() 处和
处和 ![]() 处.某时刻,监测点
处.某时刻,监测点 ![]() 收到发自目标
收到发自目标 ![]() 的一个声波,
的一个声波,![]() 后监测点
后监测点 ![]() 后监测点
后监测点 ![]() 相继收到这一信号,在当时的气象条件下,声波在水中的传播速度是
相继收到这一信号,在当时的气象条件下,声波在水中的传播速度是 ![]() .
.

(1)设 ![]() 到
到 ![]() 的距离为
的距离为 ![]() ,用
,用 ![]() 分别表示
分别表示 ![]() 到
到 ![]() 的距离,并求
的距离,并求 ![]() 的值;
的值;
(2)求目标 ![]() 的海防警戒线
的海防警戒线 ![]() 的距离(精确到
的距离(精确到 ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com