
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1 , A1D1的中点,点P,Q分别在棱DD1 , BB1上移动,且DP=BQ=λ(0<λ<2) 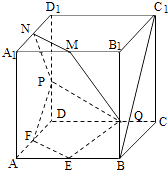
(1)当λ=1时,证明:直线BC1∥平面EFPQ;
(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.
【答案】
(1)证明:以D为原点,射线DA,DC,DD1分别为x,y,z轴的正半轴,建立坐标系,则B(2,2,0),C1(0,2,2),E(2,1,0),F(1,0,0),P(0,0,λ),
∴ ![]() =(﹣2,0,2),
=(﹣2,0,2), ![]() =(﹣1,0,λ),
=(﹣1,0,λ), ![]() =(1,1,0)
=(1,1,0)
λ=1时, ![]() =(﹣2,0,2),
=(﹣2,0,2), ![]() =(﹣1,0,1),
=(﹣1,0,1),
∴ ![]() =2
=2 ![]() ,
,
∴BC1∥FP,
∵FP平面EFPQ,BC1平面EFPQ,
∴直线BC1∥平面EFPQ;
(2)解:设平面EFPQ的一个法向量为 ![]() =(x,y,z),则
=(x,y,z),则 ![]() ,
,
∴取 ![]() =(λ,﹣λ,1).
=(λ,﹣λ,1).
同理可得平面MNPQ的一个法向量为 ![]() =(λ﹣2,2﹣λ,1),
=(λ﹣2,2﹣λ,1),
若存在λ,使面EFPQ与面PQMN所成的二面角为直二面角,则
![]()
![]() =λ(λ﹣2)﹣λ(2﹣λ)+1=0,∴λ=1±
=λ(λ﹣2)﹣λ(2﹣λ)+1=0,∴λ=1± ![]() .
.
∴存在λ=1± ![]() ,使面EFPQ与面PQMN所成的二面角为直二面角.
,使面EFPQ与面PQMN所成的二面角为直二面角.

【解析】(1)建立坐标系,求出 ![]() =2
=2 ![]() ,可得BC1∥FP,利用线面平行的判定定理,可以证明直线BC1∥平面EFPQ;(2)求出平面EFPQ的一个法向量、平面MNPQ的一个法向量,利用面EFPQ与面PQMN所成的二面角为直二面角,建立方程,即可得出结论.
,可得BC1∥FP,利用线面平行的判定定理,可以证明直线BC1∥平面EFPQ;(2)求出平面EFPQ的一个法向量、平面MNPQ的一个法向量,利用面EFPQ与面PQMN所成的二面角为直二面角,建立方程,即可得出结论.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到点
到点![]() 的距离的最大值为
的距离的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
, ![]() 为抛物线
为抛物线![]() :
: ![]() 上一动点,过点
上一动点,过点![]() 作抛物线
作抛物线![]() 的切线交椭圆
的切线交椭圆![]() 于
于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由不等式组  确定的平面区域记为Ω1 , 不等式组
确定的平面区域记为Ω1 , 不等式组 ![]() 确定的平面区域记为Ω2 , 在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
确定的平面区域记为Ω2 , 在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池![]() 的池底水平铺设污水净化管道(
的池底水平铺设污水净化管道(![]() ,
,![]() 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口![]() 是
是![]() 的中点,
的中点,![]() 分别落在线段
分别落在线段![]() 上.已知
上.已知![]() 米,
米,![]() 米,记
米,记![]() .
.
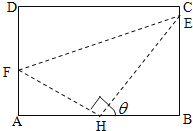
(1)试将污水净化管道的长度![]() 表示为
表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)若![]() ,求此时管道的长度
,求此时管道的长度![]() ;
;
(3)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度.
取何值时,污水净化效果最好?并求出此时管道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
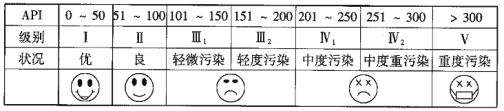
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,得到频率分布条形图如图.
进行分组,得到频率分布条形图如图.
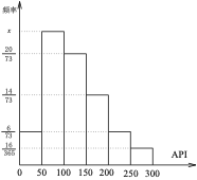
(1)求图中![]() 的值;
的值;
(2)空气质量状况分别为轻微污染或轻度污染定为空气质量Ⅲ级,求一年中空气质量为Ⅲ级的天数
(3)小张到该城市出差一天,这天空气质量为优良的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校计划在全国中学生田径比赛期间,安排6位志愿者到4个比赛场地提供服务,要求甲、乙两个比赛场地各安排一个人,剩下两个比赛场地各安排两个人,其中的小李和小王不在一起,不同的安排方案共有( )
A. 168种 B. 156种 C. 172种 D. 180种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com