【题目】已知函数
.
（1） 把
的图象上每一点的纵坐标变为原来的
倍，再将横坐标向右平移
个单位，可得
图象，求，的值；
（2） 若对任意实数
和任意
，恒有
，求实数
的取值范围.
【答案】（1） 
；（2） 
.
【解析】
（1）由图象变换规律得到
，
的值；
（2）令m＝3+2sinθcosθ，n＝asinθ+acosθ，则
，利用三角函数公式换元，即可得解.
（1）
=
.
把
的图象上每一点的纵坐标变为原来的
倍，再将横坐标向右平移
个单位，可得
图象，
∴；
（2）任意x∈R与
，有
恒成立
令m＝3+2sinθcosθ，n＝asinθ+acosθ，则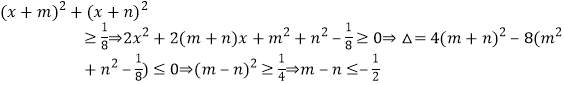
或
令t＝sinθ+cosθ2sinθcosθ＝t2﹣1且
，
即：m＝t2+2，n＝at，m﹣n＝t2﹣at+2
则：
或
参数分离求最值（注意单调区间）
由或
或
或
其中
在
上单调递减，
，当且仅当
等号成立.
由单调性可得
或
综上可得实数a的取值范围为
．
举一反三同步巧讲精练系列答案科目：高中数学 来源： 题型：
【题目】已知数列{an}，{bn}满足2Sn=（an+2）bn，其中Sn是数列{an}的前n项和．
（1）若数列{an}是首项为
，公比为-
的等比数列，求数列{bn}的通项公式；
（2）若bn=n，a2=3，求证：数列{an}满足an+an+2=2an+1，并写出数列{an}的通项公式．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2﹣ax，（a＞0）， 
，命题p：an=f（n）是递增数列，命题q：g（x）在（a，π）上有且仅有2条对称轴．
（1）求g（x）的周期和单调递增区间；
（2）若p∧q为真，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，a，b，c分别为内角A，B，C的对边，且asinB=﹣bsin（A+ 
）．
（1）求A；
（2）若△ABC的面积S= 
c2 ， 求sinC的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在菱形
中， 
， 
，以4个顶点为圆心的扇形的半径为1，若在该菱形中任意选取一点，该点落在阴影部分的概率为
，则圆周率
的近似值为（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】因为菱形的内角和为360°，
所以阴影部分的面积为半径为1的圆的面积，
故由几何概型可知
，
解得
.选C。
【题型】单选题
【结束】
12
【题目】已知函数f（x）=
，若g（x）=f（x）-a恰好有3个零点，则a的取值范围为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知y＝f(x)是定义域为R的奇函数，当x∈[0，＋∞)时，f(x)＝x2－2x.
(1)写出函数y＝f(x)的解析式
(2)若方程f(x)＝a恰有3个不同的解，求a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
