
【题目】已知函数![]() .
.
(1)讨论![]() 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若对![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)证明:若![]() ,不等式
,不等式![]() 成立.
成立.
【答案】(1)当![]() 时,函数
时,函数![]() 有两个极值点;当
有两个极值点;当![]() 时,函数
时,函数![]() 没有极值点(2)
没有极值点(2)![]() (3)证明见解析
(3)证明见解析
【解析】
(1)求导可得![]() ,转化问题为
,转化问题为![]() 的变号零点个数,分别讨论
的变号零点个数,分别讨论![]() ,
,![]() ,
,![]() 的情况即可;
的情况即可;
(2)转化问题为![]() 在
在![]() 上恒成立,设
上恒成立,设![]() ,利用导函数求得
,利用导函数求得![]() 的最小值,进而求解;
的最小值,进而求解;
(3)由(2)可得![]() 恒成立,即
恒成立,即![]() ,则欲证
,则欲证![]() ,只需证
,只需证![]() ,设
,设![]() ,进而利用导函数求得
,进而利用导函数求得![]() 的最小值大于等于0即可.
的最小值大于等于0即可.
(1)解:由题,![]()
设![]() ,令
,令![]() ,即方程
,即方程![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,此时
,此时![]() 没有极值点;
没有极值点;
当![]() 时,
时,![]() ,设方程
,设方程![]() 两根为
两根为![]() ,
,![]() ,不妨设
,不妨设![]() ,
,
则![]() ,
,![]() ,则
,则![]() ,
,
当![]() 或
或![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
此时![]() ,
,![]() 是函数
是函数![]() 的两个极值点,
的两个极值点,
当![]() 时,
时,![]() ,设方程
,设方程![]() 两根为
两根为![]() ,
,![]() ,
,
则![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ,故
,故![]() 没有极值点,
没有极值点,
综上,当![]() 时,函数
时,函数![]() 有两个极值点;当
有两个极值点;当![]() 时,函数
时,函数![]() 没有极值点.
没有极值点.
(2)解:由题,![]() 在
在![]() 上恒成立,
上恒成立,
则![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
设![]() ,
,
则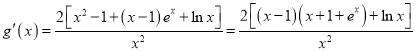 ,
,
因为![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 单调递减;当
单调递减;当![]() ,
,![]() ,则
,则![]() 单调递增;
单调递增;
所以![]() ,
,
所以![]()
(3)证明:由(2)知![]() ,所以
,所以![]() 恒成立,
恒成立,
即![]() ,
,
欲证![]() ,
,
只需证![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,则
,则![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() ,
,
所以当![]() 时,不等式
时,不等式![]() 成立.
成立.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与直线
两点,与直线![]() 相交于点
相交于点![]() ,且
,且![]() 是线段
是线段![]() 的中点,求
的中点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级![]() 四位学生
四位学生![]() 参加了文科综合知识竞赛,在竞赛结果公布前,地理老师预测得冠军的是
参加了文科综合知识竞赛,在竞赛结果公布前,地理老师预测得冠军的是![]() 或
或![]() ;历史老师预测得冠军的是
;历史老师预测得冠军的是![]() ;政治老师预测得冠军的不可能是
;政治老师预测得冠军的不可能是![]() 或
或![]() ;语文老师预测得冠军的是
;语文老师预测得冠军的是![]() ,而班主任老师看了竞赛结果后说以上只有两位老师都说对了,则得冠军的是_____。
,而班主任老师看了竞赛结果后说以上只有两位老师都说对了,则得冠军的是_____。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计的频率分布直方图如图所示.
(单位:克)中,经统计的频率分布直方图如图所示.
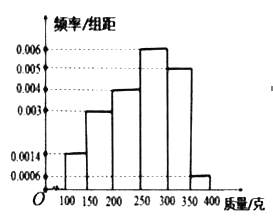
(1)估计这组数据平均数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总计,该种植园中还未摘下的芒果大约还有10000个,经销商提出以下两种收购方案:
方案①:所有芒果以9元/千克收购;
方案②:对质量低于250克的芒果以2元/个收购,对质量高于或等于250克的芒果以3元/个收购.
通过计算确定种植园选择哪种方案获利更多.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某电视台主办的歌手大奖赛上七位评委为甲、乙两名选手打出的分数的茎叶图(其中![]() 为数字0~9中的一个),则下列结论中正确的是( )
为数字0~9中的一个),则下列结论中正确的是( )
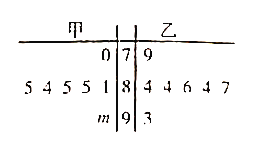
A. 甲选手的平均分有可能和乙选手的平均分相等
B. 甲选手的平均分有可能比乙选手的平均分高
C. 甲选手所有得分的中位数比乙选手所有得分的中位数低
D. 甲选手所有得分的众数比乙选手所有得分的众数高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】吸烟有害健康,远离烟草,珍惜生命。据统计一小时内吸烟5支诱发脑血管病的概率为0.02,一小时内吸烟10支诱发脑血管病的概率为0.16.已知某公司职员在某一小时内吸烟5支未诱发脑血管病,则他在这一小时内还能继吸烟5支不诱发脑血管病的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不确定
D. 不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书甲、乙、丙三人在理论考试中“合格”的概率依次为![]() ,
,![]() ,
,![]() ,在实际操作考试中“合格”的概率依次为
,在实际操作考试中“合格”的概率依次为![]() ,
,![]() ,
,![]() ,所有考试是否合格相互之间没有影响.
,所有考试是否合格相互之间没有影响.
(1)假设甲、乙、丙三人同时进行理论与实际操作两项考试,谁获得合格证书的可能性最大?
(2)这三人进行理论与实际操作两项考试后,求恰有两人获得合格证书的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角是二项式系数在三角形中的一种几何排列,是中国古代数学的杰出研究成果之一.在欧洲,左下图叫帕斯卡三角形,帕斯卡在1654年发现的这一规律,比杨辉要迟393年,比贾宪迟600年.某大学生要设计一个程序框图,按右下图标注的顺序将表上的数字输出,若第5次输出数“1”后结束程序,则空白判断框内应填入的条件为( )
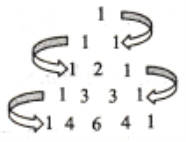
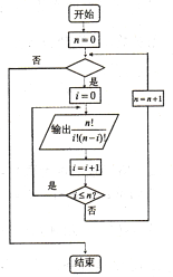
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com