练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】平面直角坐标系xoy中，直线l的参数方程是 （t为参数），以射线ox为极轴建立极坐标系，曲线C的极坐标方程是 +ρ2sin2θ=1．
    （1）求曲线C的直角坐标方程；
    （2）求直线l与曲线C相交所得的弦AB的长．

    【答案】
    （1）

    解：曲线C的极坐标方程是 +ρ2sin2θ=1，把x=ρcosθ，y=ρsinθ代入可得： =1


    （2）

    解：直线l的参数方程是 （t为参数），即 ，代入椭圆方程可得： ﹣2=0，

    ∴t1+t2= ，t1t2=﹣ ，∴|AB|=|t1﹣t2|= = =


    【解析】（1）曲线C的极坐标方程是 +ρ2sin2θ=1，把x=ρcosθ，y=ρsinθ代入可得直角坐标方程．．（2）直线l的参数方程是 （t为参数），即 ，代入椭圆方程可得： ﹣2=0，利用|AB|=|t1﹣t2|= 即可得出

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知以点A(－1,2)为圆心的圆与直线l1：x＋2y＋7＝0相切．过点B(－2,0)的动直线l与圆A相交于M，N两点，Q是MN的中点．

    (1)求圆A的方程；

    (2)当|MN|＝2时，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（12分）已知函数f(x)对任意的实数m，n都有：f(m＋n)＝f(m)＋f(n)－1，

    且当x＞0时，有f(x)＞1.

    (1)求f(0)．

    (2)求证：f(x)在R上为增函数．

    (3)若f(1)＝2，且关于x的不等式f(ax－2)＋f(x－x2)＜3对任意的x∈[1，＋∞)恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）= ，g（x）=ax3﹣x2﹣x+b（a，b∈R，a≠0），g（x）的图象C在x=﹣ 处的切线方程是y= ．
    （1）若求a，b的值，并证明：当x∈（﹣∞，2]时，g（x）的图象C上任意一点都在切线y= 上或在其下方；
    （2）求证：当x∈（﹣∞，2]时，f（x）≥g（x）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将两块三角板按图甲方式拼好，其中， ， ，

    ，现将三角板沿折起，使在平面上的射影恰好在上，如图乙．

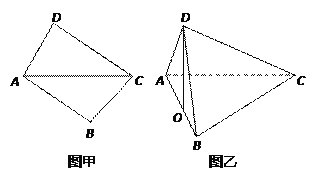
    （1）求证： ；

    （2）求证： 为线段中点；

    （3）求二面角的大小的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数y=f(x)在上是增函数，函数y=f(x+2)是偶函数，则（ ）

    A. f(1)<f(2.5)<f(3.5) B. f(3.5)<f(1)<f(2.5)

    C. f(3.5)<f(2.5)<f(1) D. f(2.5)<f(1)<f(3.5)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】锐角△ABC中，角A，B，C所对的边分别为a，b，c，且acosB+bcosA= csinC．
    （1）求cosC；
    （2）若a=6，b=8，求边c的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正项等比数列{an}满足a7=a6+2a5 ， 若存在两项am ， an使得 ，则 的最小值为（ ）
    A.
    B.
    C.
    D.不存在

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设全集U=R，集合 ，P={x|﹣1≤x≤4}，则（UM）∩P等于（ ）
    A.{x|﹣4≤x≤﹣2}
    B.{x|﹣1≤x≤3}
    C.{x|3≤x≤4}
    D.{x|3＜x≤4}

    查看答案和解析>>

    同步练习册答案