
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | | | | b | | |
| 频率 | a | 0.25 | | | | |

(1)a=0.1,b=3;4;65%.
(2)分布列为
E(X)=2.2X 1 2 3 4 P 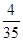
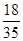
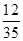
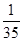
解析试题分析:(1)由[50,70)范围的频数,计算出该范围内的频率a,首先计算出[70,90)范围内的频数,然后得出[80,90),即可求出[90,100)范围内的学生人数,计算出[90,100)范围内的学生人数,然后除以20就是及格率.(2)写出随机变量X的所有可能取值,然后计算出相应的概率,列表即可的分布列,最后根据期望值公式计算期望值即可.
试题解析:(1)由茎叶图可知分数在[50,70)范围内的有2人,在[110,130) 范围内的有3人,
∴a= b=3;分数在[70,90)内的人数20×0.25=5,结合茎叶图可得分数在[70,80)内的人数为2,所以分数在[90,100)范围内的学生人数为4,故数学成绩及格的学生为13人,所以估计这次考试全校学生数学成绩的及格率为
b=3;分数在[70,90)内的人数20×0.25=5,结合茎叶图可得分数在[70,80)内的人数为2,所以分数在[90,100)范围内的学生人数为4,故数学成绩及格的学生为13人,所以估计这次考试全校学生数学成绩的及格率为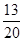 ×100%=65%.
×100%=65%.
(2)由茎叶图可知分数在[100,130)范围内的有7人,分数在[100,110)范围内的有4人,则随机变量X的所有可能取值为1,2,3,4.相应的概率为:P(X=1)=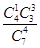 =
=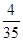 ;P(X=2)=
;P(X=2)=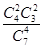 =
=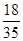 ;P(X=3)=
;P(X=3)=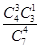 =
=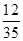 ;P(X=4)=
;P(X=4)=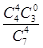 =
=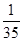 .
.
随机变量X的分布列为
E(X)=1×X 1 2 3 4 P 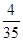
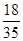
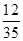
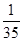
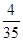 +2×
+2×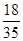 +3×
+3×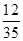 +4×
+4×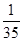 =2.2
=2.2
考点:1.茎叶图的含义以及频率和频数的计算;2.随机变量的分布列和数学期望.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
(Ⅰ)求上图中 的值;
的值;
(Ⅱ)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);
(Ⅲ)由上图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了加强中学生实践、创新能力和团队精神的培养,促进教育教学改革,市教育局举办了全市中学生创新知识竞赛,某中学举行了选拔赛,共有150名学生参加,为了了解成绩情况,从中抽取了50名学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:
(Ⅰ)完成频率分布表(直接写出结果),并作出频率分布直方图;
(Ⅱ)若成绩在95.5分以上的学生为一等奖,试估计全校获一等奖的人数,现在从全校所有一等奖的同学中随机抽取2名同学代表学校参加决赛,某班共有2名同学荣获一等奖,求该班同学参加决赛的人数恰为1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成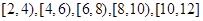 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.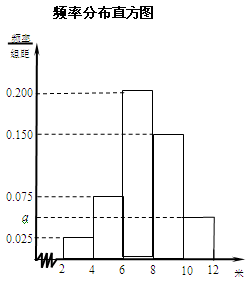
(Ⅰ)求实数 的值及参加“掷实心球”项目测试的人数;
的值及参加“掷实心球”项目测试的人数;
(Ⅱ)根据此次测试成绩的结果,试估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀的概率;
(Ⅲ)若从此次测试成绩不合格的男生中随机抽取2名学生再进行其它项目的测试,求所抽取的2名学生来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某年某省有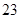 万多文科考生参加高考,除去成绩为
万多文科考生参加高考,除去成绩为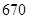 分(含
分(含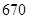 分)以上的
分)以上的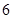 人与成绩为
人与成绩为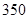 分(不含
分(不含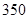 分)以下的
分)以下的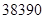 人,还有约
人,还有约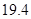 万文科考生的成绩集中在
万文科考生的成绩集中在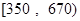 内,其成绩的频率分布如下表所示:
内,其成绩的频率分布如下表所示:
| 分数段 | 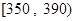 | 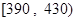 | 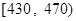 | 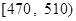 |
| 频率 | 0.108 | 0.133 | 0.161 | 0.183 |
| 分数段 | 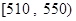 | 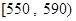 | 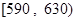 | 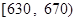 |
| 频率 | 0.193 | 0.154 | 0.061 | 0.007 |
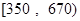 内文科考生的平均分(精确到
内文科考生的平均分(精确到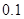 );
);查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组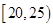 ,第2组
,第2组 ,第3组
,第3组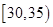 ,第4组
,第4组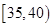 ,第5组
,第5组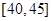 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
频率分布表
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ▓ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| | 合计 | ▓ | ▓ |
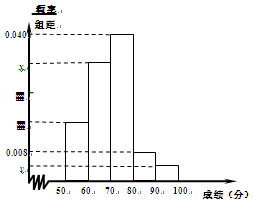
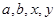 的值;
的值;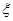 表示所抽取的2名同学中来自第5组的人数,求
表示所抽取的2名同学中来自第5组的人数,求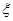 的分布列及其数学期望.
的分布列及其数学期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
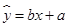 ;
; 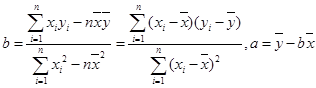 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com