
分析 令g(x)=|x+1|+|2x-1|并分段写出.
(1)直接由根式内部的代数式大于等于0求解绝对值的不等式得答案;
(2)函数f(x)的定义域为R,即|x+1|+|2x-1|-m≥0恒成立,分离参数m后求解函数g(x)的值域得答案.
解答 解:令g(x)=|x+1|+|2x-1|=$\left\{\begin{array}{l}{-3x,x≤-1}\\{2-x,-1<\frac{1}{2}≤\frac{1}{2}}\\{3x,x>\frac{1}{2}}\end{array}\right.$,
(1)当m=3时,$f(x)=\sqrt{|x+1|+|2x-1|-3}$,
由|x+1|+|2x-1|-3≥0,得$\left\{{\begin{array}{l}{x≤-1}\\{-3x-3≥0}\end{array}}\right.$,或$\left\{\begin{array}{l}-1<x≤\frac{1}{2}\\ 2-x-3≥0\end{array}\right.$,或$\left\{{\begin{array}{l}{x>\frac{1}{2}}\\{3x-3≥0}\end{array}}\right.$,
解得x≤-1,或x≥1,
故函数f(x)的定义域为{x|x≤-1,或x≥1};
(2)由题可知|x+1|+|2x-1|-m≥0恒成立,即m≤|x+1|+|2x-1|=g(x)恒成立,
由(1)知$g{(x)_{min}}=g(\frac{1}{2})=\frac{3}{2}$,故$m≤\frac{3}{2}$.
∴$m∈(-∞,\frac{3}{2}]$.
点评 本题考查函数的定义域及其求法,考查了分段函数的应用,训练了利用分离变量法求解参数的范围,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | PM2.5浓度 | 日期 | PM2.5浓度 | 日期 | PM2.5浓度 |
| 11-1 | 137 | 11-11 | 144 | 11-21 | 40 |
| 11-2 | 143 | 11-12 | 166 | 11-22 | 42 |
| 11-3 | 145 | 11-13 | 197 | 11-23 | 35 |
| 11-4 | 193 | 11-14 | 194 | 11-24 | 53 |
| 11-5 | 133 | 11-15 | 219 | 11-25 | 88 |
| 11-6 | 22 | 11-16 | 41 | 11-26 | 29 |
| 11-7 | 22 | 11-17 | 90 | 11-27 | 199 |
| 11-8 | 57 | 11-18 | 46 | 11-28 | 287 |
| 11-9 | 111 | 11-19 | 80 | 11-29 | 291 |
| 11-10 | 134 | 11-20 | 67 | 11-30 | 452 |
| 空气质量指数类别 | PM2.5 24小时浓度均值 | 频数 | 频率 |
| 优 | 0-35 | 4 | $\frac{2}{15}$ |
| 良 | 36-75 | 7 | $\frac{7}{30}$ |
| 轻度污染 | 76-115 | 4 | |
| 中度污染 | 116-150 | 6 | |
| 重度污染 | 151-250 | ||
| 严重污染 | 251-500 | ||
| 合计 | / | 30 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
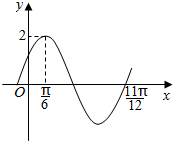 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )| A. | f(x)=2sin(x+$\frac{π}{3}$) | B. | f(x)=2sin(2x+$\frac{π}{6}$) | C. | f(x)=2sin(2x-$\frac{π}{6}$) | D. | f(x)=2sin(4x-$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com