
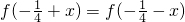 ,且f(x)<2x的解集为
,且f(x)<2x的解集为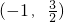
 +x)=f(-
+x)=f(- -x)
-x) 对称,可得-
对称,可得- =-
=- 即a=2b …①
即a=2b …① )
) 且a>0.
且a>0.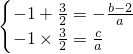 …②
…②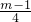
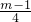 <-1时,即m<-3时,g(x)min=g(-1)=m-2
<-1时,即m<-3时,g(x)min=g(-1)=m-2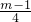 ≤2时,即-3≤m≤9时,g(x)min=g(
≤2时,即-3≤m≤9时,g(x)min=g(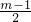 )=-4,
)=-4,
 ∈[-3,9],符合题意
∈[-3,9],符合题意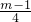 >2时,即m>9时,g(x)min=g(2)=7-2m
>2时,即m>9时,g(x)min=g(2)=7-2m <5.不符合题意
<5.不符合题意
 .
. 对称,得到a=2b,再由f(x)<2x的解集为
对称,得到a=2b,再由f(x)<2x的解集为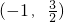 得到相应方程的根为x1=-1,x2=
得到相应方程的根为x1=-1,x2= 且a>0,结合根与系数的关系可得关于a、b、c方程组,由此联解即可得到a、b、c的值,从而得到求f(x)的解析式;
且a>0,结合根与系数的关系可得关于a、b、c方程组,由此联解即可得到a、b、c的值,从而得到求f(x)的解析式;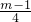 对称.因此分m<-3时、-3≤m≤9时和m>9时三种情况,根据函数的单调性列出各种情况下的最小值为4的式子,解出m的值并结合大前提进行取舍,最后综合即可得到符合题意的实数m的值.
对称.因此分m<-3时、-3≤m≤9时和m>9时三种情况,根据函数的单调性列出各种情况下的最小值为4的式子,解出m的值并结合大前提进行取舍,最后综合即可得到符合题意的实数m的值.

 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x) | x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com