
【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上表补充完整(不用写计算过程);
(2)能否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 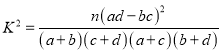 ,其中
,其中![]() )
)
科目:高中数学 来源: 题型:
【题目】某工厂的甲、乙两个车间的![]() 名工人进行了劳动技能大比拼,规定:技能成绩大于或等于
名工人进行了劳动技能大比拼,规定:技能成绩大于或等于![]() 分为优秀,
分为优秀, ![]() 分以下为非优秀,统计成成绩后,得到如下的
分以下为非优秀,统计成成绩后,得到如下的![]() 列联表,且已知在甲、乙两个车间工人中随机抽取
列联表,且已知在甲、乙两个车间工人中随机抽取![]() 人为优秀的概率为
人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲车间 |
| ||
乙车间 |
| ||
合计 |
|
(1)请完成上面的列联表;
(2)根据列联表的数据,若按![]() 的可靠性要求,能否认为“成绩与车间有关系”?
的可靠性要求,能否认为“成绩与车间有关系”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2=4,直线l:x+y=2.以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.
(1)将圆C和直线l的方程化为极坐标方程;
(2)P是l上的点,射线OP交圆C于点R,又点Q在OP上且满足|OQ|·|OP|=|OR|2,当点P在l上移动时,求点Q轨迹的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m-|x-1|-|x-2|,m∈R,且f(x+1)≥0的解集为[0,1].
(1)求m的值;
(2)若a,b,c,x,y,z∈R,且x2+y2+z2=a2+b2+c2=m,求证:ax+by+cz≤1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示
表示![]() 中的最大值,如
中的最大值,如![]() ,已知函数
,已知函数![]() .
.
(1)求函数![]() 在
在![]() 上的值域;
上的值域;
(2)试探讨是否存在实数![]() , 使得
, 使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;
的取值范围;
若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com