
【题目】已知f(x)是定义在R上的偶函数,且f(x﹣ ![]() )=f(x+
)=f(x+ ![]() )恒成立,当x∈[2,3]时,f(x)=x,则当x∈(﹣2,0)时,函数f(x)的解析式为( )
)恒成立,当x∈[2,3]时,f(x)=x,则当x∈(﹣2,0)时,函数f(x)的解析式为( )
A.|x﹣2|
B.|x+4|
C.3﹣|x+1|
D.2+|x+1|
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为  (t为参数),在以原点O为极点,x轴正半轴为极轴的极坐标系中,圆C的方程为ρ=6sinθ.
(t为参数),在以原点O为极点,x轴正半轴为极轴的极坐标系中,圆C的方程为ρ=6sinθ.
(Ⅰ)写出直线l的普通方程和圆C的直角坐标方程;
(Ⅱ)设点P(4,3),直线l与圆C相交于A,B两点,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在本校任选了一个班级,对全班50名学生进行了作业量的调查,根据调查结果统计后,得到如下的![]() 列联表,已知在这50人中随机抽取1人,认为作业量大的概率为
列联表,已知在这50人中随机抽取1人,认为作业量大的概率为![]() .
.
| 认为作业量大 | 认为作业量不大 | 合计 |
男生 | 18 | ||
女生 | 17 | ||
合计 | 50 |
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,能否有![]() 的把握认为“认为作业量大”与“性别”有关?
的把握认为“认为作业量大”与“性别”有关?
附表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | span>5.024 | 6.635 | 10.828 |
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上海中学在每学年的上学期会举行体育嘉年华活动,假设在今年的活动中共设了8个体育项目,高一某班的班主任参加了其中的若干个项目,甲、乙、丙三位同学猜测该老师参加的项目见下表:(“×”表示未参加,“√”表示参加)
项目1 | 项目2 | 项目3 | 项目4 | 项目5 | 项目6 | 项目7 | 项目8 | |
甲 | √ | × | × | × | × | √ | × | √ |
乙 | × | √ | √ | × | × | × | √ | × |
丙 | √ | × | √ | √ | √ | × | × | × |
老师告诉甲、乙、丙:“你们分别猜对5次、5次、6次”,由此请你猜测该老师参加的体育项目编号依次为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.当![]() 时,函数
时,函数![]() 在
在![]() 上有最小值;
上有最小值;
B.当![]() 时,函数
时,函数![]() 在
在![]() 上有最小值;
上有最小值;
C.对任意的实数![]() ,函数
,函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
D.方程![]() 可能有三个实数根.
可能有三个实数根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学一起去向老师询问各自的分班情况,老师说:你们四人中有![]() 位分到
位分到![]() 班,
班,![]() 位分到
位分到![]() 班,我现在给甲看乙、丙的班级,给乙看丙的班级,给丁看甲的班级.看后甲对大家说:我还是不知道我的班级,根据以上信息,则( )
班,我现在给甲看乙、丙的班级,给乙看丙的班级,给丁看甲的班级.看后甲对大家说:我还是不知道我的班级,根据以上信息,则( )
A. 乙可以知道四人的班级 B. 丁可以知道四人的班级
C. 乙、丁可以知道对方的班级 D. 乙、丁可以知道自己的班级
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD= ![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°. 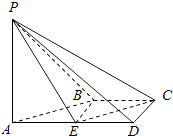
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com