
【题目】如图,四棱锥P﹣ABCD中,PD⊥平面PAB,AD∥BC,BC=CD= ![]() AD,E,F分别为线段AD,PD的中点.
AD,E,F分别为线段AD,PD的中点. 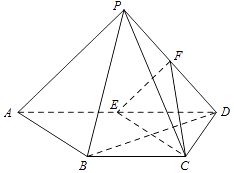
(Ⅰ)求证:CE∥平面PAB;
(Ⅱ)求证:PD⊥平面CEF;
(Ⅲ)写出三棱锥D﹣CEF与三棱锥P﹣ABD的体积之比.(结论不要求证明)
【答案】(Ⅰ)证明:∵BC∥AD,BC= ![]() ,E为AD中点,
,E为AD中点,
∴AE∥BC,且AE=BC,
∴四边形ABCE为平行四边形,
∴CE∥AB,
又AB平面PAB,CE平面PAB,
∴CE∥平面PAB.
(Ⅱ)证明:∵E、F分别为AD、PD的中点,∴EF∥PA,
又∵PD⊥平面PAB,PA,AB平面PAB,
∴PD⊥AB,PD⊥PA,∴PD⊥EF,
又CE∥AB,∴PD⊥CE,
∵EF∩CE=E,
∴PD⊥平面CEF.
(Ⅲ)解:三棱锥D﹣CEF与三棱锥P﹣ABD的体积之比为:
![]() =
= ![]() .
.
【解析】(Ⅰ)推导出四边形ABCE为平行四边形,从而CE∥AB,由此能证明CE∥平面PAB.(Ⅱ)推导出EF∥PA,则PD⊥AB,PD⊥PA,从而PD⊥EF,由CE∥AB,得PD⊥CE,由此能证明PD⊥平面CEF.(Ⅲ)由三棱锥的体积公式能求出三棱锥D﹣CEF与三棱锥P﹣ABD的体积之比.
【考点精析】掌握直线与平面平行的判定和直线与平面垂直的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N. 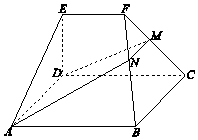
(Ⅰ)求证:AD∥MN;
(Ⅱ)求证:平面ADMN⊥平面CDEF;
(Ⅲ)若CD⊥EA,EF=ED,CD=2EF,平面ADE∩平面BCF=l,求二面角A﹣l﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女子善织,日益功,疾,初日织五尺,今一月织九匹三丈(1匹=40尺,一丈=10尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织5尺,一月织了九匹三丈,问每天增加多少尺布?”若一个月按31天算,记该女子一个月中的第n天所织布的尺数为an , 则 ![]() 的值为( )
的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个半径不等的圆盘叠放在一起(有一轴穿过它们的圆心),两圆盘上分别有互相垂直的两条直径将其分为四个区域,小圆盘上所写的实数分别记为x1 , x2 , x3 , x4 , 大圆盘上所写的实数分别记为y1 , y2 , y3 , y4 , 如图所示.将小圆盘逆时针旋转i(i=1,2,3,4)次,每次转动90° , 记Ti(i=1,2,3,4)为转动i次后各区域内两数乘积之和,例如T1=x1y2+x2y3+x3y4+x4y1 . 若x1+x2+x3+x4<0,y1+y2+y3+y4<0,则以下结论正确的是( ) 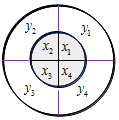
A.T1 , T2 , T3 , T4中至少有一个为正数
B.T1 , T2 , T3 , T4中至少有一个为负数
C.T1 , T2 , T3 , T4中至多有一个为正数
D.T1 , T2 , T3 , T4中至多有一个为负数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度.药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示: 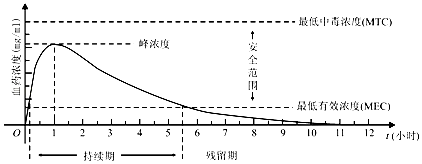
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的是( )
A.首次服用该药物1单位约10分钟后,药物发挥治疗作用
B.每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
C.每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
D.首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx﹣ ![]() )(ω>0)的图象与x轴的相邻两个交点的距离为
)(ω>0)的图象与x轴的相邻两个交点的距离为 ![]() .
.
(1)求w的值;
(2)设函数g(x)=f(x)+2cos2x﹣1,求g(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱柱ABCD﹣A1B1C1D1中,AB=1,AA1=2,点P是平面A1B1C1D1内的一个动点,则三棱锥P﹣ABC的正视图与俯视图的面积之比的最大值为( ) 
A.1
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 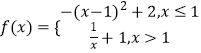 下列四个命题:
下列四个命题:
①f(f(1))>f(3); ② ![]() x0∈(1,+∞),f'(x0)=-1/3;
x0∈(1,+∞),f'(x0)=-1/3;
③f(x)的极大值点为x=1; ④ ![]() x1,x2∈(0,+∞),|f(x1)-f(x2)|≤1
x1,x2∈(0,+∞),|f(x1)-f(x2)|≤1
其中正确的有(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数y=f(x)定义域是R,当x≥0时,f(x)=x(1﹣x).
(1)求出函数y=f(x)的解析式;
(2)写出函数y=f(x)的单调递增区间.(不用证明,只需直接写出递增区间即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com