
【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了![]() 至
至![]() 月份每月
月份每月![]() 号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期 |
|
|
|
|
|
|
昼夜温差 |
|
|
|
|
|
|
就诊人数 |
|
|
|
| 16 |
|
该兴趣小组确定的研究方案是:先从这六组数据中选取![]() 组,用剩下的
组,用剩下的![]() 组数据求线性回归方程,再用被选取的
组数据求线性回归方程,再用被选取的![]() 组数据进行检验.
组数据进行检验.
(1)求选取的2组数据恰好是相邻两个月的概率;
(2)若选取的是![]() 月与
月与![]() 月的两组数据,请根据
月的两组数据,请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过![]() 人,则认为得到的线性回归方程是理想的,试问(2)中所得线性回归方程是否理想?
人,则认为得到的线性回归方程是理想的,试问(2)中所得线性回归方程是否理想?
参考公式:
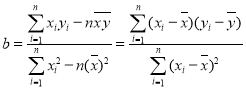 ,
,
![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)是理想的.
;(3)是理想的.
【解析】
试题分析:(1)本小题是古典概型,设到相邻两个月的数据为事件![]() ,首选任取3组数据共有15种等可能情形,事件
,首选任取3组数据共有15种等可能情形,事件![]() 含有5种情况,由古典概型概率公式可得结论;(2)由给出的公式教育处回归方程的系数
含有5种情况,由古典概型概率公式可得结论;(2)由给出的公式教育处回归方程的系数![]() 可得回归方程;(3)用(2)中回归方程估计1月份和6月份数据,即把
可得回归方程;(3)用(2)中回归方程估计1月份和6月份数据,即把![]() 和
和![]() 代入计算出估值数据,与实际数据比较可得是否理想.
代入计算出估值数据,与实际数据比较可得是否理想.
试题解析:(1)设到相邻两个月的数据为事件![]() .因为从
.因为从![]() 组数据中选取
组数据中选取![]() 组数据共有
组数据共有![]() 种情况,每种情况都是等可能出现的其中,抽到相邻两个月份的数据的情况有
种情况,每种情况都是等可能出现的其中,抽到相邻两个月份的数据的情况有![]() 种,所以
种,所以![]() .
.
(2)由数据求得![]() ,由公式求得
,由公式求得![]() ,再由
,再由![]() .
.
所以![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
(3) 当![]() 时,
时,![]() ;同样, 当
;同样, 当![]() 时,
时,![]() ,
,
所以该小组所得线性回归方程是理想的.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线经过点(0,1),求实数
处的切线经过点(0,1),求实数![]() 的值;
的值;
(Ⅱ)求证:当![]() 时,函数
时,函数![]() 至多有一个极值点;
至多有一个极值点;
(Ⅲ)是否存在实数![]() ,使得函数
,使得函数![]() 在定义域上的极小值大于极大值?若存在,求出
在定义域上的极小值大于极大值?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5;4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(I)求取出的3个球编号都不相同的概率;
(II)记![]() 为取出的3个球中编号的最小值,求
为取出的3个球中编号的最小值,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查:生产某产品需投入年固定成本为3万元,每生产![]() 万件,需另投入流动成本为
万件,需另投入流动成本为![]() 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,![]()
![]() (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,![]() (万元).通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元).通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万件)的函数解析式;
(万件)的函数解析式;
(2)写出当产量为多少时利润最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有840名职工,现采用系统抽样方法,抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间[481,720]的人数为 ( )
A. 11 B. 12
C. 13 D. 14
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中真命题的个数为( )
①平行于同一平面的两直线平形;②平行于同一平面的两个平面平行;
③垂直于同一平面的两直线平行;④垂直于同一平面的两平面垂直;
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com