练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

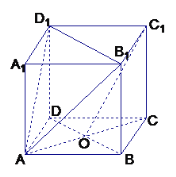
    【题目】已知正方体，是底面对角线的交点.

    求证：（1）；

    （2）CO∥面.

    【答案】（1）见解析（2）见解析

    【解析】

    （1）利用线面垂直的性质可得结合，由线面垂直的判定定理可得平面，从而可得结果；（2）连接与交点为，连接,先证明为平行四边形，可得，由线面平行的判定定理可得结论.

    （1）由题知AC⊥BD，BB1⊥平面ABCD，

    AC平面ABCD, 所以AC⊥BB1

    而BD∩BB1=B， 所以AC⊥平面BB1D1D,

    B1D1平面BB1D1D,所以AC⊥B1D1

    （2）证明：连接AC与BD交点为O，连接AO,

    由正方体知AC//AC，AC=AC，OC//AO，OC=AO

    所以OCOA为平行四边形，即　OC//AO

    又　AO在面ABD，OC不在面ABD，

    所以OC//面ABD（线线平行---线面平行）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD中，PA⊥平面ABCD，四边形ABCD是直角梯形，其中DA⊥AB，AD∥BC．PA=2AD=BC=2，AB=2 ．

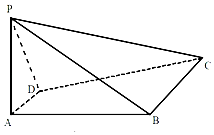
    （1）求异面直线PC与AD所成角的大小；
    （2）若平面ABCD内有一经过点C的曲线E，该曲线上的任一动点Q都满足PQ与AD所成角的大小恰等于PC与AD所成角．试判断曲线E的形状并说明理由；
    （3）在平面ABCD内，设点Q是（2）题中的曲线E在直角梯形ABCD内部（包括边界）的一段曲线CG上的动点，其中G为曲线E和DC的交点．以B为圆心，BQ为半径r的圆分别与梯形的边AB、BC交于M、N两点．当Q点在曲线段CG上运动时，试求圆半径r的范围及VP﹣BMN的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况，从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高，数据如下：(单位：cm)

    甲：9,10,11,12,10,20

    乙：8,14,13,10,12,21.

    (1)在给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图；

    (2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差，并由此判断甲、乙两种麦苗的长势情况．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（选修4﹣5：不等式选讲）
    已知函数f（x）=|2x﹣1|+|2x+a|，g（x）=x+3．
    （1）当a=﹣2时，求不等式f（x）＜g（x）的解集；
    （2）设a＞﹣1，且当 时，f（x）≤g（x），求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设f(x)是定义在R 且周期为1的函数，在区间上， 其中集合D=，则方程f(x)-lgx=0的解的个数是____________

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论函数的单调性；

    （2）若对任意，都有恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业员工500人参加“学雷锋”活动，按年龄共分六组，得频率分布直方图如下：

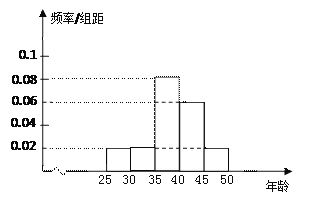
    （1）现在要从年龄较小的第1、2、3组中用分层抽样的方法抽取6人，则年龄在第1,2,3组的各抽取多少人？

    （2）在第（1）问的前提下，从这6人中随机抽取2人参加社区活动，求至少有1人年龄在第3组的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】街道旁边有一游戏:在铺满边长为9 cm的正方形塑料板的宽广地面上,掷一枚半径为1 cm的小圆板,规则如下:每掷一次交5角钱,若小圆板压在正方形的边上,可重掷一次;若掷在正方形内,须再交5角钱可玩一次;若掷在或压在塑料板的顶点上,可获得一元钱,试问:

    (1)小圆板压在塑料板的边上的概率是多少?

    (2)小圆板压在塑料板顶点上的概率是多少?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： （）的左焦点为，离心率为．

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）设为坐标原点， 为直线上一点，过作的垂线交椭圆于， ．当四边形是平行四边形时，求四边形的面积。

    查看答案和解析>>

    同步练习册答案