[题目]某市出租车的计价标准是:4km以内10元.超过4km且不超过18km的部分1.2元/km.超过18km的部分1.8元/km.不计等待时间的费用．(1)如果某人乘车行驶了10km.他要付多少车费?与行车里程x(km)的函数关系式．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】某市出租车的计价标准是：4km以内（含4km）10元，超过4km且不超过18km的部分1.2元/km，超过18km的部分1.8元/km，不计等待时间的费用．
（1）如果某人乘车行驶了10km，他要付多少车费？
（2）试建立车费y（元）与行车里程x（km）的函数关系式．

【答案】解：（1）x=10km，4km＜x≤18km，y=10+1.2﹙x﹣4）=1.2x+5.2=17.2元；
（2）由题意
0km＜x≤4km时，y=10；
4km＜x≤18km时，y=10+1.2﹙x﹣4﹚，即y=1.2x+5.2；
x＞18km时，y=10+1.214+1.8﹙x﹣18﹚即y=1.8x﹣5.6，
所以车费与行车里程的函数关系式为y=．
【解析】（1）x=10km，4km＜x≤18km，y=10+1.2﹙x﹣4）；
（2）利用条件，可得分段函数．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在四棱锥中，平面平面，侧面是边长为的等边三角形，底面是矩形，且，则该四棱锥外接球的表面积等于__________.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，已知四棱锥，，侧面是边长为4的等边三角形，底面为菱形，侧面与底面所成的二面角为.

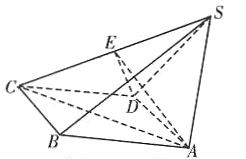
（1）求点到平面的距离；

（2）若为的中点，求二面角的正弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数

（Ⅰ）当时，求函数的单调区间；

（Ⅱ）当，时，证明：（其中为自然对数的底数）.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标平面中，的两个顶点为，平面内两点、同时满足：①；②；③．

（1）求顶点的轨迹的方程；

（2）过点作两条互相垂直的直线，直线与点的轨迹相交弦分别为，设弦的中点分别为．

①求四边形的面积的最小值；

②试问：直线是否恒过一个定点？若过定点，请求出该定点，若不过定点，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某校高三年级共有学生195人，其中女生105人，男生90人.现采用按性别分层抽样的方法，从中抽取13人进行问卷调查．设其中某项问题的选择分别为“同意”、“不同意”两种，且每人都做了一种选择．下面表格中提供了被调查人答卷情况的部分信息．

	同意	不同意	合计
女学生	4
男学生		2

（Ⅰ）完成上述统计表；

（Ⅱ）根据上表的数据估计高三年级学生该项问题选择“同意”的人数；

（Ⅲ）从被抽取的女生中随机选取2人进行访谈，求选取的2名女生中至少有一人选择“同意”的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知圆C：x2+y2﹣2x+4my+4m2=0，圆C1：x2+y2=25，以及直线l：3x﹣4y﹣15=0．
（1）求圆C1：x2+y2=25被直线l截得的弦长；
（2）当m为何值时，圆C与圆C1的公共弦平行于直线l；
（3）是否存在m，使得圆C被直线l所截的弦AB中点到点P（2，0）距离等于弦AB长度的一半？若存在，求圆C的方程；若不存在，请说明理由．