
【题目】已知函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(2)已知正数![]() 满足:存在
满足:存在![]() ,使得
,使得![]() 成立.试比较
成立.试比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】分析:(1)设![]() ,不等式
,不等式![]() 可化为
可化为![]()
![]() ,对
,对![]() 可把
可把![]() 作为一个整体,分子分母同除以
作为一个整体,分子分母同除以![]() ,转化后可利用基本不等式求得其最值,从而得
,转化后可利用基本不等式求得其最值,从而得![]() 的范围;
的范围;
(2)令函数![]() ,则
,则![]() ,由导数可求得
,由导数可求得![]() 的最小值,而题中命题成立,即这个最小值
的最小值,而题中命题成立,即这个最小值![]() ,从而可得
,从而可得![]() 的取值范围,而比较
的取值范围,而比较![]() 与
与![]() ,即比较
,即比较![]() 与
与![]() 的大小,即比较
的大小,即比较![]() 与
与![]() 的大小.于是可构造函数
的大小.于是可构造函数![]() (
(![]() ),利用导数得出其单调性,从而得结论.
),利用导数得出其单调性,从而得结论.
详解:(1)由条件知![]() 在
在![]() 上恒成立,
上恒成立,
令![]() (
(![]() ),则
),则![]() ,所以
,所以![]() 对于任意
对于任意![]() 成立.
成立.
因为![]() ,∴
,∴![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
因此实数![]() 的取值范围是
的取值范围是![]() .
.
(2)令函数![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,又
,又![]() ,故
,故![]() ,
,
所以![]() 是
是![]() 上的单调递增函数,
上的单调递增函数,
因此![]() 在
在![]() 上的最小值是
上的最小值是![]() .
.
由于存在![]() ,使
,使![]() 成立,当且仅当最小值
成立,当且仅当最小值![]() ,
,
故![]() ,即
,即![]() .
.
![]() 与
与![]() 均为正数,同取自然底数的对数,
均为正数,同取自然底数的对数,
即比较![]() 与
与![]() 的大小,试比较
的大小,试比较![]() 与
与![]() 的大小.
的大小.
构造函数![]() (
(![]() ),则
),则![]() ,
,
再设![]() ,
,![]() ,从而
,从而![]() 在
在![]() 上单调递减,
上单调递减,
此时![]() ,故
,故![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 在
在![]() 上单调递减.
上单调递减.
综上所述,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且x≤0时, f(x)=-x+1
(1)求f(0),f(2);
(2)求函数f(x)的解析式;
(3)若f(a-1)<3,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究变量![]() ,
,![]() 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论
①残差平方和越小的模型,拟合的效果越好;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小说明拟合效果越好;
越小说明拟合效果越好;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均增加0.2个单位
平均增加0.2个单位
④若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强,以上正确说法的个数是( )
之间的负相关很强,以上正确说法的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生物学家预言,21世纪将是细菌发电造福人类的时代。说起细菌发电,可以追溯到1910年,英国植物学家利用铂作为电极放进大肠杆菌的培养液里,成功地制造出世界上第一个细菌电池。然而各种细菌都需在最适生长温度的范围内生长。当外界温度明显高于最适生长温度,细菌被杀死;如果在低于细菌的最低生长温度时,细菌代谢活动受抑制。为了研究某种细菌繁殖的个数![]() 是否与在一定范围内的温度
是否与在一定范围内的温度![]() 有关,现收集了该种细菌的6组观测数据如下表:
有关,现收集了该种细菌的6组观测数据如下表:

经计算得:![]() ,
,![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]() .其中
.其中![]() 分别为观测数据中的温度与繁殖数,
分别为观测数据中的温度与繁殖数,![]() .
.
参考数据:![]() ,
,![]() ,
,
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (精确到0.1);
(精确到0.1);
(Ⅱ)若用非线性回归模型求得![]() 关于
关于![]() 回归方程为
回归方程为![]() ,且非线性回归模型的残差平方和
,且非线性回归模型的残差平方和![]() .
.
(ⅰ)用相关指数![]() 说明哪种模型的拟合效果更好;
说明哪种模型的拟合效果更好;
(ⅱ)用拟合效果好的模型预测温度为34℃时该种细菌的繁殖数(结果取整数).
附:一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计为
的斜率和截距的最小二乘法估计为 ,
,![]() ;
;
相关指数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂每日生产一种产品![]() 吨,每日生产的产品当日销售完毕,日销售额为
吨,每日生产的产品当日销售完毕,日销售额为![]() 万元,产品价格随着产量变化而有所变化,经过一段时间的产销,得到了
万元,产品价格随着产量变化而有所变化,经过一段时间的产销,得到了![]() ,
,![]() 的一组统计数据如下表:
的一组统计数据如下表:

(1)请判断![]() 与
与![]() 中,哪个模型更适合刻画
中,哪个模型更适合刻画![]() ,
,![]() 之间的关系?可从函数增长趋势方面给出简单的理由;
之间的关系?可从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并估计当日产量
的回归方程,并估计当日产量![]() 时,日销售额是多少?
时,日销售额是多少?
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
线性回归方程![]() 中,
中,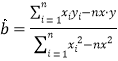 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com