
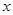 的实系数方程
的实系数方程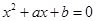 有两个根,一个根在区间
有两个根,一个根在区间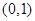 内,另一根在区间
内,另一根在区间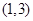 内,记点
内,记点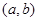 对应的区域为
对应的区域为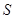 .
.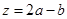 ,求
,求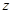 的取值范围;
的取值范围;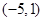 的一束光线,射到
的一束光线,射到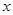 轴被反射后经过区域
轴被反射后经过区域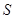 ,求反射光线所在直线
,求反射光线所在直线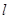 经过区域
经过区域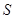 内的整点(即横纵坐标为整数的点)时直线
内的整点(即横纵坐标为整数的点)时直线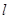 的方程.
的方程.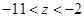 ;(2)
;(2)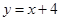 。
。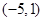 的光线经
的光线经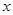 轴反射后的光线必过点
轴反射后的光线必过点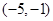 ,再结合(1)中的可行域先观察可能满足条件的整点,逐个验证,最终找到符合条件的整点.进而确定所求直线的方程.
,再结合(1)中的可行域先观察可能满足条件的整点,逐个验证,最终找到符合条件的整点.进而确定所求直线的方程.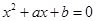 的两根在区间
的两根在区间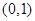 和
和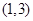 上的几何意义是:函数
上的几何意义是:函数
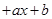 与
与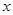 轴的两个交点的横坐标分别在区间
轴的两个交点的横坐标分别在区间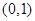 和
和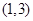 内,由此可得不等式组
内,由此可得不等式组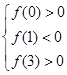 ,即
,即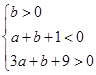 ,则在坐标平面
,则在坐标平面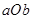 内,点
内,点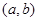 对应的区域
对应的区域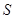 如图阴影部分所示,
如图阴影部分所示,
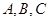 三点的坐标分别为
三点的坐标分别为 ,......4分
,......4分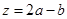 ,则直线
,则直线 经过点
经过点 时
时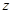 取得最小值,经过点
取得最小值,经过点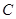 时
时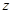 取得最大值,即
取得最大值,即 ,
,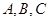 三点的值没有取到,所以
三点的值没有取到,所以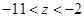 ;......8分
;......8分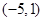 的光线经
的光线经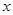 轴反射后的光线必过点
轴反射后的光线必过点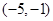 ,由图可知
,由图可知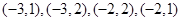 ,再结合不等式知点
,再结合不等式知点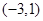 符合条件,所以此时直线方程为:
符合条件,所以此时直线方程为: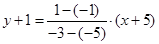 ,即
,即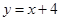 .......11分
.......11分

科目:高中数学 来源:不详 题型:解答题
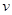 千米/时
千米/时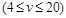 从A地出发到相距50千米的
从A地出发到相距50千米的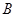 地去,然后乘汽车以匀速
地去,然后乘汽车以匀速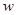 千米/时
千米/时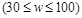 自
自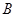 地向相距300千米的C地驶去,要求在当天16:00时至21:00时这段时间到达C地.设汽车所需要的时间为
地向相距300千米的C地驶去,要求在当天16:00时至21:00时这段时间到达C地.设汽车所需要的时间为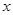 小时, 摩托车所需要的时间为
小时, 摩托车所需要的时间为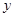 小时.
小时.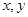 的约束条件;
的约束条件;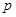 ,且
,且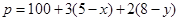 (元),那么
(元),那么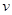 ,
, 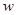 分别是多少时所要的经费最少?此时需花费多少元?
分别是多少时所要的经费最少?此时需花费多少元?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com