
已知函数 ,
, 的最大值是1,最小正周期是
的最大值是1,最小正周期是 ,其图像经过点
,其图像经过点 .
.
(1)求 的解析式;
的解析式;
(2)设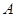 、
、 、
、 为△ABC的三个内角,且
为△ABC的三个内角,且 ,
, ,求
,求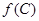 的值.
的值.
(1)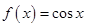 ;(2)
;(2)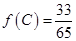 .
.
【解析】
试题分析:(1)根据题中的已知条件确定函数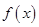 中各未知量的值进而求出函数
中各未知量的值进而求出函数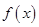 的解析式;(2)在求出函数
的解析式;(2)在求出函数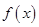 的解析式
的解析式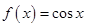 之后,利用三角形的内角和定理,将
之后,利用三角形的内角和定理,将 的值转化为
的值转化为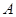 与
与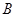 的和角的三角函数来求解,具体转化思路为
的和角的三角函数来求解,具体转化思路为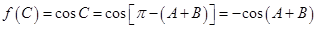 ,然后再利用同角三角函数之间的关系以及两角和的余弦公式进行求值.
,然后再利用同角三角函数之间的关系以及两角和的余弦公式进行求值.
试题解析:(1)因为函数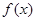 的最大值是1,且
的最大值是1,且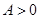 ,所以
,所以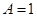 .
.
因为函数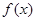 的最小正周期是
的最小正周期是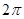 ,且
,且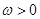 ,所以
,所以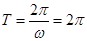 ,解得
,解得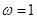 .
.
所以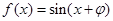 .因为函数
.因为函数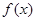 的图像经过点
的图像经过点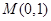 ,所以
,所以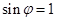 .
.
因为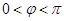 ,所以
,所以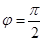 .所以
.所以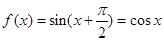 .
.
(2)由(1)得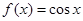 ,所以
,所以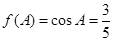 ,
, .
.
因为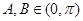 ,所以
,所以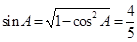 ,
,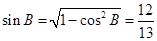 .
.
因为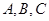 为△ABC的三个内角,所以
为△ABC的三个内角,所以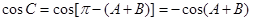 .
.
所以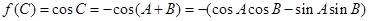
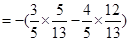
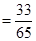 .
.
考点:三角函数的基本性质、两角和的余弦函数、同角三角函数之间的关系


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com